... (1930)¹

actually Bloch (1929) came with it first, but Dirac is popularly blamed.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... components²

Please, excuse my notation here. I use ``hats'' above operators/potentials (e.g., $\hat{V}_{ext}$ is the external potential) and no ``hats'' above the corresponding energy components (e.g. $V_{ext}$ is the energy corresponding to external potential). The exception is a hamiltonian for which $\hat{H}$ is the operator, while $E$ is the value of energy. This may add confusion, since in much of the literature energy components are denoted with capital letters or subscripted $E$'s, while the operators are in capital letters, and potentials in lowercase letters. But this notation also leads to a conflict with notation for one-particle operators, which are written often in lower case.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...$\rho({\bf r})$³

actually, in the original HK paper, and many papers with a physical slant, the density is denoted as $n({\bf r})$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

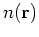... optimized⁴

it also needs to be constrained by v-representability, but we still do not know how to express v-representability in a closed mathematical form. There exist, however, methods, e.g., constrained search (Levy, 1982) and local-scaling transformation (Petkov et al, 1986) which assure v-representability during density optimization, though their algorithmic implementation needs to be done.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... equation⁵

if expansion into basis sets is used, the matrix equation (57) for expansion coefficients is identical as in Hartree-Fock method.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

... field⁶

It has to be stressed that 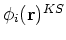$\phi_i({\bf r})^{KS}$'s are not the real orbitals, and they do not correspond to a real physical system. Their only role in the theory is to provide a mapping between kinetic energy and density. For one, the total KS wave function is a single determinant and is unable to model situations where more determinants are needed to describe the system (e.g., for cases when molecules dissociate to atoms). Interesting discussion about the symmetry of this wave function is given by Dunlap (1991, 1994). More studies are needed to asses physical relevance of these orbitals.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.

...$T_0$⁷

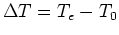$\Delta T = T_e - T_0$ is embedded in $E_{xc}$.

.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.