Introduction to Molecular Approaches of Density Functional Theory
Ohio Supercomputer Center, 1224 Kinnear Rd, Columbus, OH 43221-1153
Return to index
Density Functional Theory
For many years, the use of electron density as a fundamental
description of the system was based on intuition rather than
hard proof that this can be done. Electron density is more
attractive (depends only on x,y,z, and eventually, there may be
two densities for spin polarized systems, one for spin up electrons
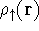 and one for spin down electrons
and one for spin down electrons 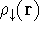 ,
as opposed to many particle
wave function which depends on all coordinates of all particles, i.e.,
for N electrons, it depends on 3N variables (or 4N
if you count in spin).
The fact that the ground state properties are functionals of the
electron density
,
as opposed to many particle
wave function which depends on all coordinates of all particles, i.e.,
for N electrons, it depends on 3N variables (or 4N
if you count in spin).
The fact that the ground state properties are functionals of the
electron density 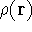 was proved by Hohenberg and Kohn (1964)
and it provides the basic framework for modern Density Functional
methods.
was proved by Hohenberg and Kohn (1964)
and it provides the basic framework for modern Density Functional
methods.
More specifically, according to the theorem proved by them, the total
ground state energy of an electron system can be written as a functional
of the electronic density, and this energy is at minimum if the density is
an exact density for the groud state. The theorem of HK is an existence
proof of such a functional, but there is no prescription how to construct it.
If we knew the form of this functional accurately, and if it was
not complicated, quantum chemistry would be a done deal.
Unfortunately we do not know the exact form of energy functional.
It is necessary to use approximations regarding parts of
the functional dealing with kinetic energy and exchange and correlation
energies of the system of electrons.
The simplest approximation is the
local density approximation (LDA) which leads to a Thomas-Fermi
(Fermi, 1928; Thomas, 1927) term
for kinetic energy (for review see, e.g., Jones & Gunnarsson, 1989;
Slater, 1968; March, 1957) and the Dirac (1930) term for the exchange
energy. The corresponding functional is called
Thomas-Fermi-Dirac energy. As you see, these developments are not recent and were parallel to the
work done in the wave function approaches. These functionals can be further improved but the results
are not that encouraging for molecular systems. But, on the other hand, the
Thomas-Fermi-Dirac+improvments method is a true density functional method, since all components of
energy are expressed via density alone, without using many particle wave functions.
However, for the time being, it seems that there is no way to avoid wave functions in molecular
calculations and for accurate calculations they have to be used as a mapping step between
the energy and density. For example, the Thomas-Fermii theory does not predict chemical bonds.
While "pure" density functional theories are very usefull in studying solid phase (e.g., conductivity), they
fail to provide meaningful results for molecular systems.
term for the exchange
energy. The corresponding functional is called
Thomas-Fermi-Dirac energy. As you see, these developments are not recent and were parallel to the
work done in the wave function approaches. These functionals can be further improved but the results
are not that encouraging for molecular systems. But, on the other hand, the
Thomas-Fermi-Dirac+improvments method is a true density functional method, since all components of
energy are expressed via density alone, without using many particle wave functions.
However, for the time being, it seems that there is no way to avoid wave functions in molecular
calculations and for accurate calculations they have to be used as a mapping step between
the energy and density. For example, the Thomas-Fermii theory does not predict chemical bonds.
While "pure" density functional theories are very usefull in studying solid phase (e.g., conductivity), they
fail to provide meaningful results for molecular systems.
The predecessor of the modern chemical approaches to the DFT was undoubtely the
Slater's X 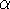 method formulated in 1951 (Slater, 1951 & 1974, for review see:
Johnson 1973 & 1975). It was
developed as an approximate solution to the HF equations.
In this method, the HF exchange was approximated by:
method formulated in 1951 (Slater, 1951 & 1974, for review see:
Johnson 1973 & 1975). It was
developed as an approximate solution to the HF equations.
In this method, the HF exchange was approximated by:
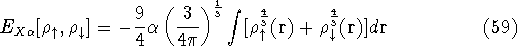
The exchange energy  is given here are a functional of densities for spin up (
is given here are a functional of densities for spin up (  ) and
spin down (
) and
spin down (  ) electrons and contains an adjustable parameter
) electrons and contains an adjustable parameter 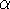 . This parameter, was empirically
optimized for each atom of the periodic table (see, e.g., Slater, 1974, Schwartz, 1972 & 1974)
and its value was between 0.7-0.8 for most atoms. For a special case of homogenous electron gas, its value
is exactly
. This parameter, was empirically
optimized for each atom of the periodic table (see, e.g., Slater, 1974, Schwartz, 1972 & 1974)
and its value was between 0.7-0.8 for most atoms. For a special case of homogenous electron gas, its value
is exactly  /
/ 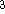 (Gáspár, 1954).
(Gáspár, 1954).
Return to index
Next Section
 term for the exchange
energy. The corresponding functional is called
Thomas-Fermi-Dirac energy. As you see, these developments are not recent and were parallel to the
work done in the wave function approaches. These functionals can be further improved but the results
are not that encouraging for molecular systems. But, on the other hand, the
Thomas-Fermi-Dirac+improvments method is a true density functional method, since all components of
energy are expressed via density alone, without using many particle wave functions.
However, for the time being, it seems that there is no way to avoid wave functions in molecular
calculations and for accurate calculations they have to be used as a mapping step between
the energy and density. For example, the Thomas-Fermii theory does not predict chemical bonds.
While "pure" density functional theories are very usefull in studying solid phase (e.g., conductivity), they
fail to provide meaningful results for molecular systems.
term for the exchange
energy. The corresponding functional is called
Thomas-Fermi-Dirac energy. As you see, these developments are not recent and were parallel to the
work done in the wave function approaches. These functionals can be further improved but the results
are not that encouraging for molecular systems. But, on the other hand, the
Thomas-Fermi-Dirac+improvments method is a true density functional method, since all components of
energy are expressed via density alone, without using many particle wave functions.
However, for the time being, it seems that there is no way to avoid wave functions in molecular
calculations and for accurate calculations they have to be used as a mapping step between
the energy and density. For example, the Thomas-Fermii theory does not predict chemical bonds.
While "pure" density functional theories are very usefull in studying solid phase (e.g., conductivity), they
fail to provide meaningful results for molecular systems.
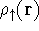 and one for spin down electrons
and one for spin down electrons 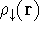 ,
as opposed to many particle
wave function which depends on all coordinates of all particles, i.e.,
for N electrons, it depends on 3N variables (or 4N
if you count in spin).
The fact that the ground state properties are functionals of the
electron density
,
as opposed to many particle
wave function which depends on all coordinates of all particles, i.e.,
for N electrons, it depends on 3N variables (or 4N
if you count in spin).
The fact that the ground state properties are functionals of the
electron density 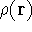 was proved by Hohenberg and Kohn (1964)
and it provides the basic framework for modern Density Functional
methods.
was proved by Hohenberg and Kohn (1964)
and it provides the basic framework for modern Density Functional
methods.
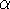 method formulated in 1951 (Slater, 1951 & 1974, for review see:
Johnson 1973 & 1975). It was
developed as an approximate solution to the HF equations.
In this method, the HF exchange was approximated by:
method formulated in 1951 (Slater, 1951 & 1974, for review see:
Johnson 1973 & 1975). It was
developed as an approximate solution to the HF equations.
In this method, the HF exchange was approximated by:
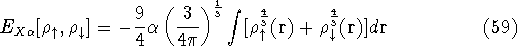
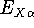 is given here are a functional of densities for spin up (
is given here are a functional of densities for spin up ( 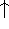 ) and
spin down (
) and
spin down ( 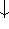 ) electrons and contains an adjustable parameter
) electrons and contains an adjustable parameter  /
/ 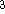 (Gáspár, 1954).
(Gáspár, 1954).