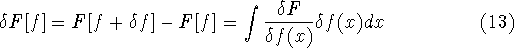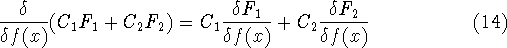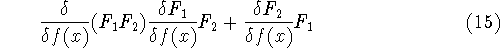Introduction to Molecular Approaches of Density Functional Theory
Ohio Supercomputer Center, 1224 Kinnear Rd, Columbus, OH 43221-1153
Return to index
Function, Operator, Functional
Before we move any further, let us introduce a few definitions.
FUNCTION
Functions is a prescription which maps one or more
numbers to another number.
For example: take a number and multiply it by itself: 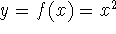 , or
take two numbers and add them together: z = g(x, y) = x + y.
Sometimes function does not have a value for some numbers, and only
certain numbers can be used as an argument for a function. E.g., square root
is only defined for nonnegative numbers (if you want to have a real number as
a result).
, or
take two numbers and add them together: z = g(x, y) = x + y.
Sometimes function does not have a value for some numbers, and only
certain numbers can be used as an argument for a function. E.g., square root
is only defined for nonnegative numbers (if you want to have a real number as
a result).
OPERATOR
Operator (usually written with a hat, e.g., 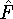 or in
calligraphic style
or in
calligraphic style 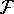 ) is
a prescription which maps one function to another function.
For example: take a function and square its value:
) is
a prescription which maps one function to another function.
For example: take a function and square its value:
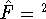 , e.g.,
, e.g., 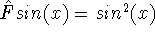 . Or
calculate second derivative of a function versus
x:
. Or
calculate second derivative of a function versus
x: 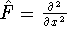 , and
, and
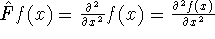 .
Nabla is a popular differenial operator in 3 dimensions. In cartesians it is:
.
Nabla is a popular differenial operator in 3 dimensions. In cartesians it is:
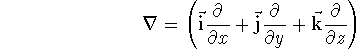
It is used to calculate forces (which are vectors),
i.e., gradients of potential energy: 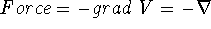 .
Its square is called laplacian, and
represents the sum of second derivatives:
.
Its square is called laplacian, and
represents the sum of second derivatives:
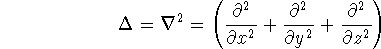
The 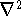 or
or 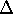 appears in the kinetic energy operator.
The prescription of forming the quantum mechanical operators, are called Jordan rules.
For cartesian coordinate representation (coordinate space), they are obtained as follows:
appears in the kinetic energy operator.
The prescription of forming the quantum mechanical operators, are called Jordan rules.
For cartesian coordinate representation (coordinate space), they are obtained as follows:
- 1.
- write a classical expression for the physical quantity and rearrange it
in such a way, that everything depends either on coordinates, or momenta (e.g., if
something depends on the component of velocity,
 , change it to
, change it to 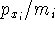 ).
).
- 2.
- replace coordinates with the operators of multuplying by the coordinate:



- 3.
- replace components of momenta with their operators:
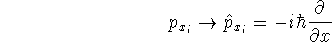
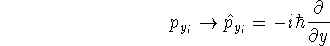
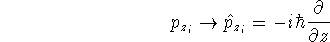
The operators can also be obtained in momentum space - the physicists like them this
way very much. Chemists are interested more in where is the electron, rather than
how fast it moves, so they use coordinate space representation as a rule.
The Schrödinger equation (1) is an example of an eigenproblem, i.e., the
equation in which an operator acts on a function and as a result it returns
the same function multiplied by a constant. For some operators, there are no
nontrivial solutions (trivial means: 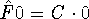 ),
but for operators which correspond to some physical
quantity of some physical system, these equations
have solutions in principle, i.e., one can find a set of
functions, and corresponding constants, which satisfy them.
While these eigenproblems
have solutions in principle, these equations may not be
easy to solve. They frequently have the form of partial second order
differential equations, or integro-differential equations, and they
may not be analytically solved in general, some special cases
may have an analytic solution (e.g., one particle, or two particles
which interact in a special way).
),
but for operators which correspond to some physical
quantity of some physical system, these equations
have solutions in principle, i.e., one can find a set of
functions, and corresponding constants, which satisfy them.
While these eigenproblems
have solutions in principle, these equations may not be
easy to solve. They frequently have the form of partial second order
differential equations, or integro-differential equations, and they
may not be analytically solved in general, some special cases
may have an analytic solution (e.g., one particle, or two particles
which interact in a special way).
FUNCTIONAL
Functional takes a function and provides a number. It is usually
written with the function in square brackets as F[f] = a. For example:
take a function and integrate it from 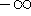 to
to 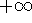 :
:
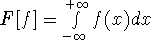 . Note that the formula for
the expectation value (3) is the total energy functional
. Note that the formula for
the expectation value (3) is the total energy functional
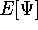 , since it takes some function
, since it takes some function 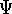 and returns the value of
energy for this
and returns the value of
energy for this 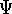 .
.
Functionals can also have derivatives, which behave similarly to
traditional derivatives for functions. The differential of the functional is
defined as:
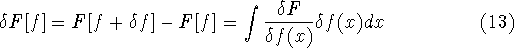
The functional derivatives have properties similar to traditional function
derivatives, e.g.:
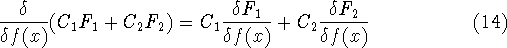
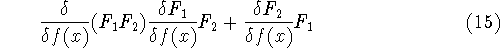
Return to index
Next Section
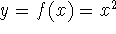 , or
take two numbers and add them together: z = g(x, y) = x + y.
Sometimes function does not have a value for some numbers, and only
certain numbers can be used as an argument for a function. E.g., square root
is only defined for nonnegative numbers (if you want to have a real number as
a result).
, or
take two numbers and add them together: z = g(x, y) = x + y.
Sometimes function does not have a value for some numbers, and only
certain numbers can be used as an argument for a function. E.g., square root
is only defined for nonnegative numbers (if you want to have a real number as
a result).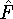 or in
calligraphic style
or in
calligraphic style 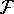 ) is
a prescription which maps one function to another function.
For example: take a function and square its value:
) is
a prescription which maps one function to another function.
For example: take a function and square its value:
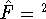 , e.g.,
, e.g., 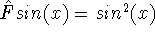 . Or
calculate second derivative of a function versus
x:
. Or
calculate second derivative of a function versus
x: 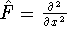 , and
, and
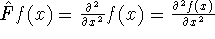 .
Nabla is a popular differenial operator in 3 dimensions. In cartesians it is:
.
Nabla is a popular differenial operator in 3 dimensions. In cartesians it is:
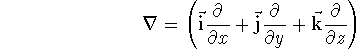
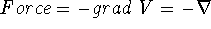 .
Its square is called laplacian, and
represents the sum of second derivatives:
.
Its square is called laplacian, and
represents the sum of second derivatives:
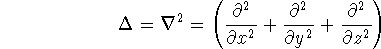
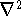 or
or 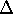 appears in the kinetic energy operator.
The prescription of forming the quantum mechanical operators, are called Jordan rules.
For cartesian coordinate representation (coordinate space), they are obtained as follows:
appears in the kinetic energy operator.
The prescription of forming the quantum mechanical operators, are called Jordan rules.
For cartesian coordinate representation (coordinate space), they are obtained as follows:
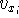 , change it to
, change it to 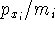 ).
).



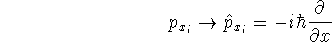
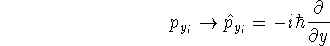
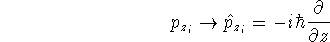
 ),
but for operators which correspond to some physical
quantity of some physical system, these equations
have solutions in principle, i.e., one can find a set of
functions, and corresponding constants, which satisfy them.
While these eigenproblems
have solutions in principle, these equations may not be
easy to solve. They frequently have the form of partial second order
differential equations, or integro-differential equations, and they
may not be analytically solved in general, some special cases
may have an analytic solution (e.g., one particle, or two particles
which interact in a special way).
),
but for operators which correspond to some physical
quantity of some physical system, these equations
have solutions in principle, i.e., one can find a set of
functions, and corresponding constants, which satisfy them.
While these eigenproblems
have solutions in principle, these equations may not be
easy to solve. They frequently have the form of partial second order
differential equations, or integro-differential equations, and they
may not be analytically solved in general, some special cases
may have an analytic solution (e.g., one particle, or two particles
which interact in a special way).
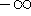 to
to 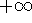 :
:
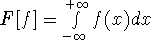 . Note that the formula for
the expectation value (
. Note that the formula for
the expectation value (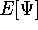 , since it takes some function
, since it takes some function 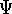 and returns the value of
energy for this
and returns the value of
energy for this