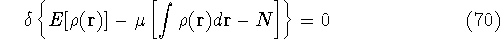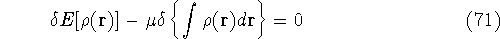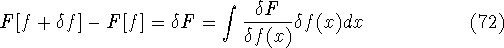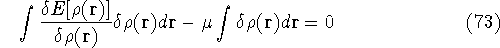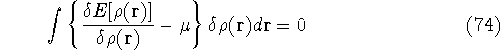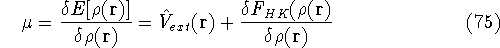Introduction to Molecular Approaches of Density Functional Theory
Ohio Supercomputer Center, 1224 Kinnear Rd, Columbus, OH 43221-1153
Return to index
Hohenberg and Kohn theorems
The field of rigorous density functional theory was born in 1964 with
the publication of the Hohenberg and Kohn paper (1964).
They proved the following:
- I.
- Every observable of a stationary quantum mechanical system (including energy), can
be calculated, in principle exactly, from the ground-state density alone, i.e.,
every observable can be written as a functional of the ground-state density.
- II.
- The ground state density can be calculated, in principle exactly,
using the variational method involving only density,
The original theorems refer to the time independent (stationary) ground state, but
are being extended to excited states and time-dependent potentials (for review see, e.g.,
Gross & Kurth, 1994).
How these theorems were derived? By quite an original logic. Within a Born-Oppenheimer
approximation, the ground state of the system of electrons is a result of positions of
nuclei. This is obvious, if we look at the  hamiltonian in equation (20).
In this hamiltonian, the kinetic energy of electrons (
hamiltonian in equation (20).
In this hamiltonian, the kinetic energy of electrons (  ) and the
electron-electron interaction (
) and the
electron-electron interaction ( 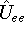 ) ``adjust'' themselves to the external
(i.e., coming from nuclei) potential
) ``adjust'' themselves to the external
(i.e., coming from nuclei) potential 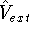 . Once the
. Once the 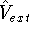 is in place,
everything else is, including electron density, which simply adjusts itself to give the
lowest possible total energy of the system. The external potential
is in place,
everything else is, including electron density, which simply adjusts itself to give the
lowest possible total energy of the system. The external potential 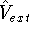 is the
only variable term in this equation, and everything else depends indirectly on it.
is the
only variable term in this equation, and everything else depends indirectly on it.
Hohenberg and Kohn posed a more interesting question, which is quite opposite to
the traditional logic: Is 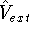 uniquely determined
from the knowledge of electron density
uniquely determined
from the knowledge of electron density 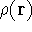 ? Can we find out (in principle,
though it need not be easy) where and what the nuclei are, if we know the density
? Can we find out (in principle,
though it need not be easy) where and what the nuclei are, if we know the density 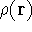 in the ground state? Is there a precise mapping from
in the ground state? Is there a precise mapping from 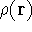 to
to 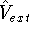 ? The answer to
this question is: Yes!. Actually the mapping is accurate within a constant, which would not
change anything, since Schrödinger equations with
? The answer to
this question is: Yes!. Actually the mapping is accurate within a constant, which would not
change anything, since Schrödinger equations with 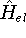 and
and 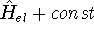 yields
exactly the same eigenfunctions, i.e., states (it is easy to prove based on the linear property
of the hamiltonian), and the energies will be simply elevated by the value of this const. Note that
all energies are known only within some constant, which establishes the frame of reference (e.g.,
we do not include electron-Mars gravitational attraction within most calculations).
yields
exactly the same eigenfunctions, i.e., states (it is easy to prove based on the linear property
of the hamiltonian), and the energies will be simply elevated by the value of this const. Note that
all energies are known only within some constant, which establishes the frame of reference (e.g.,
we do not include electron-Mars gravitational attraction within most calculations).
Why was this question so important? Because, if this is true, the knowledge
of density provides total information about the system, and formally if we know the density,
we know everything there is to known.
Since 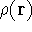 determines number of electrons, N:
determines number of electrons, N:
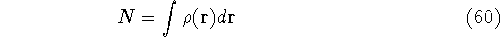
and 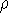 determines the
determines the 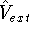 , the knowledge of total density is as good, as
knowledge of
, the knowledge of total density is as good, as
knowledge of 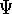 , i.e., the wave function describing the state of the system.
They proved it through a contradiction:
, i.e., the wave function describing the state of the system.
They proved it through a contradiction:
- 1.
- Assume that we have an exact ground state density
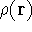 ,
,
- 2.
- Assume that the ground state is nondegenerate (i.e., there is only one wave function
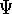 for this ground state (though HK theorems can be easily
extended for degenerate ground
states, see, e.g., Dreizler & Gross, 1990; Kohn, 1985),
for this ground state (though HK theorems can be easily
extended for degenerate ground
states, see, e.g., Dreizler & Gross, 1990; Kohn, 1985),
- 3.
- Assume that for the density
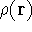 there are two possible external potentials:
there are two possible external potentials:
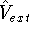 and
and 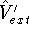 , which obviously produce two different hamiltonians:
, which obviously produce two different hamiltonians:
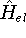 and
and 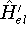 , respectively. They obviously produce two different
wave functions for the ground state:
, respectively. They obviously produce two different
wave functions for the ground state: 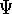 and
and 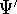 , respectively. They correspond to
energies:
, respectively. They correspond to
energies:
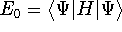 and
and 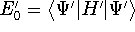 ,
respectively.
,
respectively.
- 4.
- Now, let us calculate the expectation value of energy
for the
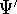 with the
hamiltonian
with the
hamiltonian 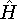 and use variational theorem:
and use variational theorem:
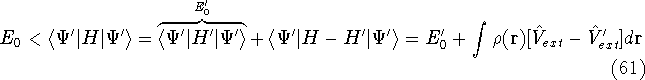
- 5.
- Now let us calculate the expectation value of energy for the
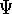 with the
hamiltonian
with the
hamiltonian 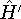 and use varational theorem:
and use varational theorem:
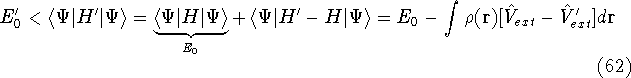
- 6.
- By adding equations (61) and (62) by sides we obtain:
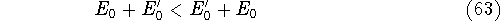
and it leads to a contradiction.
Since now, we know that 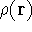 determines N and
determines N and 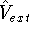 , it also
determines all properties of the ground state, including the kinetic
energy of electrons
, it also
determines all properties of the ground state, including the kinetic
energy of electrons
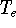 and energy of interaction among electrons
and energy of interaction among electrons 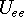 , i.e., the total ground state energy
is a functional of density with the following
components
, i.e., the total ground state energy
is a functional of density with the following
components :
:
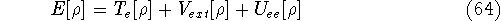
Additionally, HK grouped together all functionals
which are secondary (i.e., which are responses)
to the 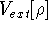 :
:
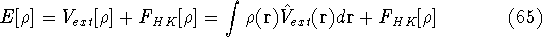
The 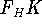 functional operates only on density and is universal, i.e., its form does not depend on the particular
system under consideration (note that N-representable densities integrate to N, and the information about
the number of electrons can be easily obtained from the density itself).
functional operates only on density and is universal, i.e., its form does not depend on the particular
system under consideration (note that N-representable densities integrate to N, and the information about
the number of electrons can be easily obtained from the density itself).
The second HK theorem provides variational principle in electron density representation 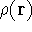
 .
For a trial density
.
For a trial density 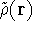 such that
such that 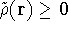 and for which
and for which
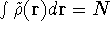 ,
,

where 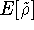 is the energy functional. In other words, if some density represents the correct number
of electrons N, the total energy calculated from this density cannot be lower than the true energy of the
ground state.
is the energy functional. In other words, if some density represents the correct number
of electrons N, the total energy calculated from this density cannot be lower than the true energy of the
ground state.
As to the necessary conditions for this theorem, there is still some controversy concerning
the, so called, representability of density. The N-representability, i.e., the fact that the trial 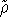 has to
sum up to N electrons is easy to achieve by simple rescaling. It is
automatically insured if
has to
sum up to N electrons is easy to achieve by simple rescaling. It is
automatically insured if 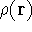 can be mapped to some wave function
(for further discussion see: Parr & Yang, 1989; Gilbert, 1975; Lieb, 1982;
and Harriman, 1980).
Assuring that the trial density has also
can be mapped to some wave function
(for further discussion see: Parr & Yang, 1989; Gilbert, 1975; Lieb, 1982;
and Harriman, 1980).
Assuring that the trial density has also 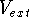 -representability
(usually denoted in the literature as v-representability) is not that easy. Levy (1982) and Lieb (1983)
have shown, that there are some ``reasonable'' trial densities, which are not the ground state densities for any
possible
-representability
(usually denoted in the literature as v-representability) is not that easy. Levy (1982) and Lieb (1983)
have shown, that there are some ``reasonable'' trial densities, which are not the ground state densities for any
possible 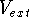 potential, i.e., they do not map to any external potential. Such densities do not correspond therefore
to any ground state, and their optimization will not lead to a ground state.
Moreover, during energy minimization, we may take a wrong turn, and get
stuck into some non v-representable density and never be able to converged
to a physically relevant ground state density.
For an interesting discussion, see
Hohenberg et al. (1990). Assuming that we restrict ourselved only to
trial densities which are both N and v representable, the variational principle for density is easly proven, since
each trial density
potential, i.e., they do not map to any external potential. Such densities do not correspond therefore
to any ground state, and their optimization will not lead to a ground state.
Moreover, during energy minimization, we may take a wrong turn, and get
stuck into some non v-representable density and never be able to converged
to a physically relevant ground state density.
For an interesting discussion, see
Hohenberg et al. (1990). Assuming that we restrict ourselved only to
trial densities which are both N and v representable, the variational principle for density is easly proven, since
each trial density 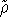 defines a hamiltonian
defines a hamiltonian 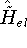 . From the hamiltonian
we can derive the corresponding wave function
. From the hamiltonian
we can derive the corresponding wave function 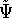 for the ground state represented by this hamiltonian. And
according to the traditional variational principle, this wave function
for the ground state represented by this hamiltonian. And
according to the traditional variational principle, this wave function 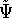 will not be a ground state
for the hamiltonian of the real system
will not be a ground state
for the hamiltonian of the real system 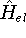 :
:
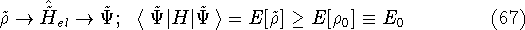
where 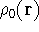 is the true ground state density of the real system.
is the true ground state density of the real system.
The condition of minimum for the energy functional:
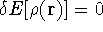 needs to be constrained
by the N-representability of density which is optimized
needs to be constrained
by the N-representability of density which is optimized .
The Lagrange's method of undetermined multipliers is a very
convenient approach for the constrained minimization
problems. In this method
we represent constraints in such a way that their value is
exactly zero when they are satisfied. In our case, the
N representability constraint can be represented as:
.
The Lagrange's method of undetermined multipliers is a very
convenient approach for the constrained minimization
problems. In this method
we represent constraints in such a way that their value is
exactly zero when they are satisfied. In our case, the
N representability constraint can be represented as:
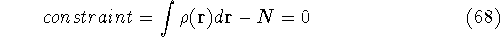
These constraints are then multiplied by an undetermined
constants and added to a minimized function or functional.
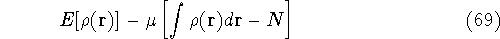
where 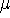 is yet undetermined Lagrange multiplier.
Now, we look for the minimum of this expression by requiring that its
differential is equal to zero (a necessary condition of minimum).
is yet undetermined Lagrange multiplier.
Now, we look for the minimum of this expression by requiring that its
differential is equal to zero (a necessary condition of minimum).
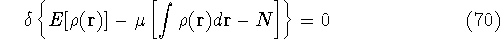
Solving this differential equation will provide us with a prescription of
finding a minimum which satisfies the constraint. In our case it leads to:
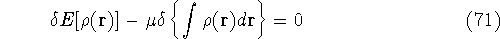
since 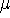 and N are constants. Using the definition of the
differential of the functional (see, e.g., Parr & Yang, 1989):
and N are constants. Using the definition of the
differential of the functional (see, e.g., Parr & Yang, 1989):
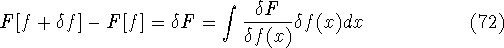
and the fact that differential and integral signs may be interchanged, we obtain
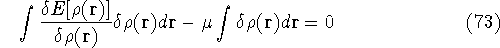
Since integration runs over the same variable and has the same limits, we can
write both expressions under the same integral:
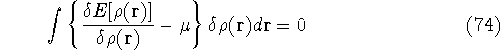
which provides the condition for constrained minimisation and defines the value
of the Lagrange multiplier at minium. It is also expressed here via external potential from equation (65):
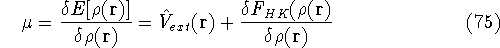
Density functional theory
gives a firm definition of the chemical potential 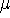 , and leads to
several important general conclusions. For review, please refer to Parr & Yang (1989), chapters 4 and 5.
, and leads to
several important general conclusions. For review, please refer to Parr & Yang (1989), chapters 4 and 5.
Return to index
Next Section
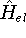 hamiltonian in equation (20).
In this hamiltonian, the kinetic energy of electrons (
hamiltonian in equation (20).
In this hamiltonian, the kinetic energy of electrons ( 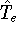 ) and the
electron-electron interaction (
) and the
electron-electron interaction ( 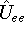 ) ``adjust'' themselves to the external
(i.e., coming from nuclei) potential
) ``adjust'' themselves to the external
(i.e., coming from nuclei) potential 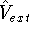 . Once the
. Once the 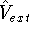 is in place,
everything else is, including electron density, which simply adjusts itself to give the
lowest possible total energy of the system. The external potential
is in place,
everything else is, including electron density, which simply adjusts itself to give the
lowest possible total energy of the system. The external potential 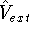 is the
only variable term in this equation, and everything else depends indirectly on it.
is the
only variable term in this equation, and everything else depends indirectly on it.
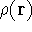 ? Can we find out (in principle,
though it need not be easy) where and what the nuclei are, if we know the density
? Can we find out (in principle,
though it need not be easy) where and what the nuclei are, if we know the density 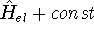 yields
exactly the same eigenfunctions, i.e., states (it is easy to prove based on the linear property
of the hamiltonian), and the energies will be simply elevated by the value of this const. Note that
all energies are known only within some constant, which establishes the frame of reference (e.g.,
we do not include electron-Mars gravitational attraction within most calculations).
yields
exactly the same eigenfunctions, i.e., states (it is easy to prove based on the linear property
of the hamiltonian), and the energies will be simply elevated by the value of this const. Note that
all energies are known only within some constant, which establishes the frame of reference (e.g.,
we do not include electron-Mars gravitational attraction within most calculations).
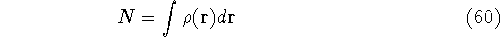
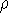 determines the
determines the 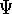 , i.e., the wave function describing the state of the system.
They proved it through a contradiction:
, i.e., the wave function describing the state of the system.
They proved it through a contradiction:
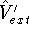 , which obviously produce two different hamiltonians:
, which obviously produce two different hamiltonians:
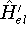 , respectively. They obviously produce two different
wave functions for the ground state:
, respectively. They obviously produce two different
wave functions for the ground state: 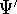 , respectively. They correspond to
energies:
, respectively. They correspond to
energies:
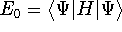 and
and 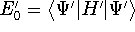 ,
respectively.
,
respectively.
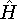 and use variational theorem:
and use variational theorem:
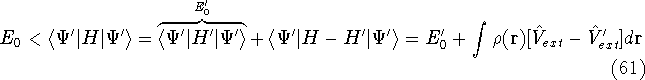
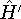 and use varational theorem:
and use varational theorem:
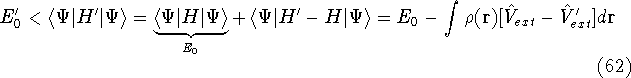
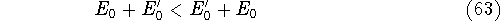
 and energy of interaction among electrons
and energy of interaction among electrons 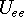 , i.e., the total ground state energy
is a functional of density with the following
components
, i.e., the total ground state energy
is a functional of density with the following
components :
:
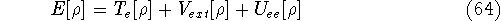
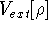 :
:
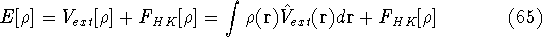
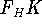 functional operates only on density and is universal, i.e., its form does not depend on the particular
system under consideration (note that N-representable densities integrate to N, and the information about
the number of electrons can be easily obtained from the density itself).
functional operates only on density and is universal, i.e., its form does not depend on the particular
system under consideration (note that N-representable densities integrate to N, and the information about
the number of electrons can be easily obtained from the density itself).
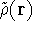 such that
such that 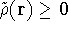 and for which
and for which
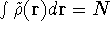 ,
,

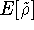 is the energy functional. In other words, if some density represents the correct number
of electrons N, the total energy calculated from this density cannot be lower than the true energy of the
ground state.
is the energy functional. In other words, if some density represents the correct number
of electrons N, the total energy calculated from this density cannot be lower than the true energy of the
ground state.
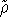 has to
sum up to N electrons is easy to achieve by simple rescaling. It is
automatically insured if
has to
sum up to N electrons is easy to achieve by simple rescaling. It is
automatically insured if 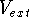 -representability
(usually denoted in the literature as v-representability) is not that easy. Levy (1982) and Lieb (1983)
have shown, that there are some ``reasonable'' trial densities, which are not the ground state densities for any
possible
-representability
(usually denoted in the literature as v-representability) is not that easy. Levy (1982) and Lieb (1983)
have shown, that there are some ``reasonable'' trial densities, which are not the ground state densities for any
possible 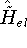 . From the hamiltonian
we can derive the corresponding wave function
. From the hamiltonian
we can derive the corresponding wave function 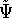 for the ground state represented by this hamiltonian. And
according to the traditional variational principle, this wave function
for the ground state represented by this hamiltonian. And
according to the traditional variational principle, this wave function 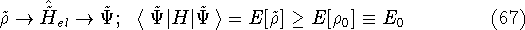
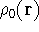 is the true ground state density of the real system.
is the true ground state density of the real system.
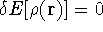 needs to be constrained
by the N-representability of density which is optimized
needs to be constrained
by the N-representability of density which is optimized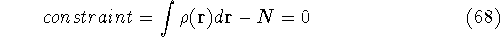
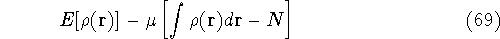
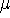 is yet undetermined Lagrange multiplier.
Now, we look for the minimum of this expression by requiring that its
differential is equal to zero (a necessary condition of minimum).
is yet undetermined Lagrange multiplier.
Now, we look for the minimum of this expression by requiring that its
differential is equal to zero (a necessary condition of minimum).