Magnetism arises from moving charges, such as an electric current in a coil of wire. In a material which does not have a current present, there are still magnetic interactions. Atoms are made of charged particles (protons and electrons) which are moving constantly. The processes which create magnetic fields in an atom are
Measurement of interactions with nuclear spins are used to analyze compounds in nuclear magnetic resonance (NMR) and electron spin resonance (ESR) spectroscopy. In most other situations, interaction with nuclear spins is a very minor effect.
Interactions between the intrinsic spin of one electron and the intrinsic spin of another electron are strongest for very heavy elements such as the actinides. This is called spin-spin coupling. For these elements this coupling can shift the electron orbital energy levels.
The interaction between an electron's intrinsic spin and it's orbital motion is called spin-orbit coupling. Spin-orbit coupling has a significant effect on the energy levels of the orbitals in many inorganic compounds.
Macroscopic effects, such as the attraction of a piece of iron to a bar magnet are primarily due to the number of unpaired electrons in the compound and their arrangement. The various possible cases are called magnetic states of matter.
Paramagnet - A paramagnetic compound will have some electrons with unpaired spins. Paramagnetic compounds are attracted by a magnet.
Ferromagnet - In a ferromagnetic substance there are unpaired electron spins, which are held in alignment by a process known as ferromagnetic coupling. Ferromagnetic compounds, such as iron, are strongly attracted to magnets.
Ferrimagnet - Ferrimagnetic compounds have unpaired electron spins, which are held in an pattern with some up and some down. This is known as ferrimagnetic coupling. In a ferrimagnetic compound, there are more spins held in one direction, so the compound is attracted to a magnet.
Antiferromagnetic - When unpaired electrons are held in an alignment with an equal number of spins in each direction, the substance is strongly repelled by a magnet. This is referred to as an antiferromagnet.
Superconductor - Superconductors are repelled by magnetic fields because the magnetic field is excluded from passing through them. This property of superconductors, called the Meissner effect, is used to test for the presence of a superconducting state. The underlying theory of how superconductivity arises is still a matter of much research and debate at the time of this writing. It does appear that the mechanism behind the magnetic properties of superconductors is significantly different from the other classes of compounds discussed here. For these reasons, superconductors will not be discussed further here.
When a material is placed in a magnetic field, the magnetic field inside the material will be the sum of the external magnetic field and the magnetic field generated by the material itself. The magnetic field in a material is called the magnetic induction and given the symbol "B". The formula for this is
B = H + 4 Pi M
where
B = magnetic induction
H = external magnetic field
Pi = 3.14159
M = magnetization ( a property of the material )
For mathematical and experimental convenience this equation if often
written as
B = 1 + 4 Pi M = 1 + 4 Pi Xv
- ------
H H
where
Xv = M/H = volume magnetic susceptibility
The volume magnetic susceptibility is so named because B, H and M
are defined per unit volume. However this results in Xv being unitless.
It is convenient to use the magnetic susceptibility instead of the
magnetization because the magnetic susceptibility is independent of the
magnitude of the external magnetic field, H, for diamagnetic and
paramagnetic materials. Many studies are done using Xg, magnetic susceptibility per gram, which is Xv divided by the density. This gives units of cm cubed per gram.
Another useful form is Xm, molar magnetic susceptibility, which is Xg times the molecular weight. This gives units of cm cubed per mole.
Another measure of magnetic interaction that is often used is an effective magnetic moment, mu, where
mu = 2.828 ( Xm T )1/2
where
mu = effective magnetic moment
Xm = molar magnetic susceptibility
T = temperature
The numeric factor puts mu in units of Bohr magnetons (BM). Where
one BM equals 9.274 x 10^-24 joules per tesla. The effective magnetic
moment is a convenient measure of a material's magnetic properties because
it is independent of temperature as well as external field strength
for diamagnetic and paramagnetic materials.This said, we would now like to examine how the magnetization, magnetic susceptibility and effective magnetic moment depend on molecular structure.
In this orbital model, the diamagnetic susceptibility from a given electron is proportional to the square of it's mean distance from the nucleus. Thus larger atoms are expected to have a larger diamagnetic interaction than smaller atoms. Often, the contributions for common atoms are tabulated along with corrections for multiple bonds. Thus a magnetic susceptibility can be predicted merely by adding together the contributions from all of the atoms and bonds in the molecule. For an example of these scheme, see Drago. For a more complete treatment, see Selwood.
mu = g { S ( S + 1 ) }1/2
where
mu = effective magnetic moment
g = 2.0023
S = 1/2 for one unpaired electron
1 for two unpaired electrons
3/2 for three unpaired electrons, etc.
This equation is sometimes written with g=2. This does not introduce a
significant error since this simple spin only treatment is a decent
approximation but is often not accurate even to two significant digits.An equation which takes into account both spin and orbital motion of the electrons is
mu = { 4 S ( S + 1 ) + L ( L + 1 ) }1/2
where
mu = effective magnetic moment
S = 1/2 for one unpaired electron, 1 for two, etc.
L = total orbital angular momentum
This equation is derived for atoms. It is applicable only to molecules
with very high symmetry where the energies of the orbitals containing
unpaired electrons are degenerate. A discussion of the calculation of
"L" can be found in any introductory quantum mechanics text or in the
chapter on quantum mechanics in many physical chemistry texts.If the splitting of orbital energy levels is large relative to k T ( k is the Boltzman constant ) then the applicable formula is
mu = g { J ( J + 1 ) }1/2
where
g = 1 + S ( S + 1 ) - L ( L + 1 ) + J ( J + 1 )
---------------------------------------
2 J ( J + 1 )
where
J = S + L
This formula is usually used for the lanthanide and actinide elements.
For more accurate treatment of these elements, a diamagnetic contribution
can be added to this as described by Selwood.If the splitting of orbital energy levels is comparable in magnitude to k T then the expression for magnetic properties must incorporate a Boltzman distribution. This is often the case with high spin transition metal complexes. The worst case, where this procedure is absolutely imperative, is the description of spin cross overs such as exhibited by some iron coordination compounds. Examples of this type of treatment are given in both the Drago and Selwood texts.
For all of the cases of paramagnetic behavior the spin only formula is often used as a first rough approximation. If the only purpose for measuring the magnetic susceptibility is to determine the number of unpaired electrons this is often all that is done.
All three of these classes of materials can be considered a special case of paramagnetic behavior. The description of paramagnetic behavior is based on the assumption that every molecule behaves independently. The materials discussed here result from a situation in which the direction of the magnetic field produced by one molecule is affected by the direction of the magnetic field produced by an adjacent molecule, in other words their behavior is coupled. If this occurs in a way in which the magnetic fields all tend to align in the same direction, a ferromagnetic material results and the phenomenon is called ferromagnetic coupling. Antiferromagnetic coupling gives an equal number of magnetic fields in opposite directions. Ferrimagnetic coupling gives magnetic fields in two opposite orientations with more in one direction than in the other.
With a few exceptions, the magnetic moments are not aligned through out the entire material. Typically regions, called domains, will form with different orientations. The existence of domains of coupled molecules gives rise to a number of types of behavior as described in the following paragraphs.
The tendency of molecules to align themselves to one another enhances the magnetization of the material due to the presence of an external magnetic field. This is why ferromagnetic and ferrimagnetic materials can have magnetic susceptibilities several orders of magnitude large than paramagnetic materials. This also gives rise to the fact that the magnetic susceptibility of these materials is not independent of the magnitude of the external magnetic field as was the case for diamagnetic and paramagnetic materials.
For a ferromagnetic material, the actual field acting on a given magnetic dipole ( unpaired electron ) is designated Ht and given by an equation similar to the equation for magnetic induction given above.
Ht = H + Nw M
where
Ht = magnetic field felt by an electron
H = external magnetic field
Nw = molecular field constant, approximately 10000
M = magnetization
This equation is used because it allows a mathematical treatment of
a ferromagnetic substance similar to that used for paramagnetic substances.
In this form the molecular field constant, Nw, is typically defined
empirically in order to take the ferromagnetic coupling into account.
To obtain the molecular field constant in a rigorous way would require
a quantum mechanical calculation that takes into account the elements,
their arrangement in the solid, kinetic energy of the electrons, coulombic
attraction of electrons to the nucleus and repulsion with other electrons
as well as spin interactions. What is most often done is a computer
simulation using the Ising model, which is not truly rigorous but is based on
quantum mechanics. This is a spin only quantum mechanical treatment assuming
that the values of neighboring spins can be replaced by their average over time.
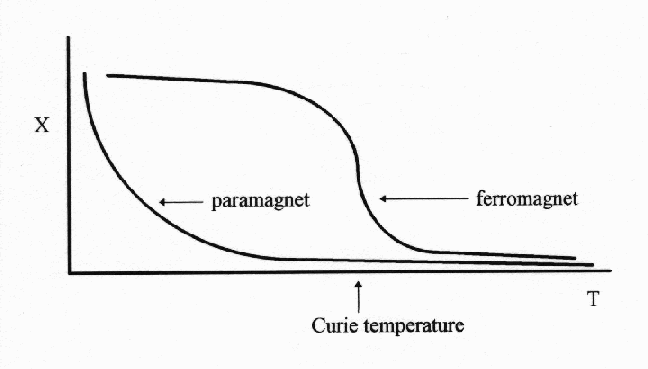
For more explanation, see Morrish.Vibrational motion of the molecules, which increases with temperature, can disrupt the domain structure. Thus the magnetic properties of all three of these types of materials are strongest at low temperatures. At sufficiently high temperatures, no domain structure is able to form so all of these materials become paramagnetic at high temperatures. The temperature at which paramagnetic behavior is seen called the Curie temperature for ferromagnetic and ferrimagnetic materials and called the Neel temperature for antiferromagnetic materials. This is why a temperature independent effective magnetic moment cannot be defined for these materials.
The alignment of the magnetic moments of the domains may give the material a net magnetic moment even in the absence of an external field. This gives a permanent magnet, such as a bar magnet. A material with no net moment prior to being exposed to an external magnetic field may retain a net moment after being exposed to an external magnetic field. This is how cassette and video tapes and computer disks store information. The magnitude of this memory effect can be quantified by plotting magnetization vs field strength as the external field intensity is varied from one polarity to the other and back again. A strong memory effect will be indicated by a wide hysteresis loop.
Over a period of time magnetic domains tend to return to a random orientation. This makes the kinetics of this relaxation process another factor in the magnetic behavior of these materials. This is also responsible for the limited life span of magnetically stored music, video and computer data.
In some paramagnetic compounds the magnetic susceptibility is inversely proportional to the temperature. These are called "normal paramagnets" and have magnetic properties arising primarily due to the presence of permanent magnetic dipoles. This is referred to as the Curie Law and is expressed in mathematical form as
X = C / T where C = Na g2 b2 ------- 4 k where X = magnetic susceptibility C = the Curie constant T = temperature Na = Avogadro's number g = the electron g factor b = the Bohr magneton k = the Boltzman constantIn most paramagnetic compounds, an inverse relationship is observed, but the extrapolation to zero temperature does not obey the Curie Law. These compounds obey the Curie-Weiss Law which is
X = C --------- T - thetawhere theta is a constant referred to as the Weiss constant. The Weiss constant can have a large range of values from -70 K to 3000 K. Most often it is positive.

When a critical temperature ( called the Curie temperature ) is reached, the curvature of the plot changes. At the Curie temperature, ferromagnetic and ferrimagnetic compounds become paramagnetic. Curie temperatures range from 16 C for Gd to 1131 C for Co.
For ferromagnetic substances a universal temperature curve can be constructed, meaning that all substances with the same total spin follow the same curve. This is done by plotting M(T)/M(0) vs T/Tc where M(T) is the magnetization at a given temperature, M(0) is the magnetization at absolute zero, T is the temperature and Tc is the Curie temperature. For more information, see Morrish.
As with ferromagnetic substances, a universal temperature curve can be constructed that all substances with the same number of unpaired electrons follow. This is done by plotting X(T)/X(Tn) vs T/Tn where X(T) is the magnetic susceptibility at a given temperature, X(Tn) is the magnetic susceptibility at the Neel temperature, T is the temperature and Tn is the Neel temperature. For more information, see Morrish.
An old but good book on many aspects of magnetochemistry is
P. W. Selwood "Magnetochemistry" Interscience (1956)
Another good text is
A. H. Morrish "The Physical Principles of Magnetism" John Wiley & Sons
(1965)
There are chapters on magnetochemistry in
R. S. Drago "Physical Methods For Chemists" Saunders College and Harcourt
Brace Jovanovich (1992)
L. Solymar, D. Walsh "Lectures on the Electrical Properties of
Materials" Oxford (1993)
A mathematical treatment can be found in
D. L. Goodstein "States of Matter" Dover (1985)
Solid state properties are covered in
A. R. West "Solid State Chemistry and its Applications" John Wiley & Sons
(1992)
A book describing more sophisticated simulation techniques is
M. H. Krieger "Constitutions of Matter" University of Chicago Press
(1996)