Polar (an abbreviation for Polarography) is a general electrochemical simulator. It analytically and digitally simulates voltammograms (polarograms) on virtually any mechanism at 9 electrode geometries (planar, spherical, semi-spherical, cylindrical, semi-cylindrical, microdisc, thin film, and rotating electrodes) in over 5 techniques (linear sweep and CV, DC, normal pulse, differential pulse, and square wave voltammetries). It also simulates effects of charge current, resistance, noise, electrolyte, stripping time, stripping potential, convection, etc. User can type in his mechanism with any symbol.

It analyses any ASCII x-y data for detecting peak location, peak value, semi-derivative, derivative, integral, semi-integral, curve fitting, and separating overlapped peaks.

It shows tip when the user put mouse cursor over a label. The program can separate overlapped voltammograms into individuals, and extract real peak from voltammogram with noise and baseline. It outputs the theoretical peak values, the peak current and potential and current-potential data, which can be imported into other program (e.g. Lotus 123). User can copy-and-paste the voltammogram into his document.

It has been successfully applied to fit experimental polarograms (voltammograms) of In(III), Cd(II), Pb(II), Tl(I), Cr(III), Zn(II), and binuclear copper complex in aqueous and non-aqueous media at mercury, solid metal and non-metal electrodes (specifically the dropping mercury, hanging mercury drop, gold, platinum and glassy carbon electrodes) by various electrochemical techniques (differential pulse, square wave, and pseudo-derivative normal pulse polarographies) [1-5].

It is available from the author or my Web site. If you have any question, please read FAQ in its document. For tutorial, please read the course practices in the rmit.htm file.

It is assumed that you agree the Shareware license that you should register by US$20 with author in 20 days or you should delete it.

<big>Chapter 2

Polarography and Voltammetry
</big>

2.1 Introduction

Modern electrochemical methods offer the analytical chemist a wide variety of techniques to solve analytical problems. Voltammetry is one such method, in which the current is measured as a function of applied potential. Polarography is another method, which differs from voltammetry in that it employs a dropping mercury electrode (DME) to continuously renew the electrode surface.

In this chapter, the fundamental principles of direct current polarography (DCP), alternating current polarography (ACP), square wave polarography (SWP), normal pulse polarography (NPP), differential pulse polarography (DPP), and pseudo-derivative normal pulse polarography (PDNPP) are reviewed. Much of this theory is also applicable to voltammetry. Linear sweep voltammetry (LSV) and stripping voltammetry (SV) are also described. If you are familiar with polarography and voltammetry, they can move directly to the next chapter.

Beside techniques, theoretical equations also depend on mechanism, reversibility, and electrode geometry. You can calculate the limiting current from the below equations by clicking the Theoretical Peak submenu.

2.2 Direct Current Polarography

Heyrovsky invented the original polarographic method, conventional direct current polarography (DCP), and Heyrovsky and Shikata constructed the first polarograph in 1925 [6]. DCP involves the measurement of current flowing through the dropping mercury electrode (DME) as a function of applied potential. Under the influence of gravity, mercury drops grow from the end of a fine glass capillary until they detach. Then the process is allowed to repeat itself. Drops may be allowed to fall naturally or may be dislodged after a specified interval with the aid of a mechanical device. A major advantage of the DME is that a constantly renewed electrode surface is exposed to the test solution so that problems of electrode blockage are avoided. Another advantage of the DME is that it allows a number of electrode reduction processes to be monitored, which would otherwise be inaccessible, because a wide negative potential region is available on account of the high overpotential for water reduction.

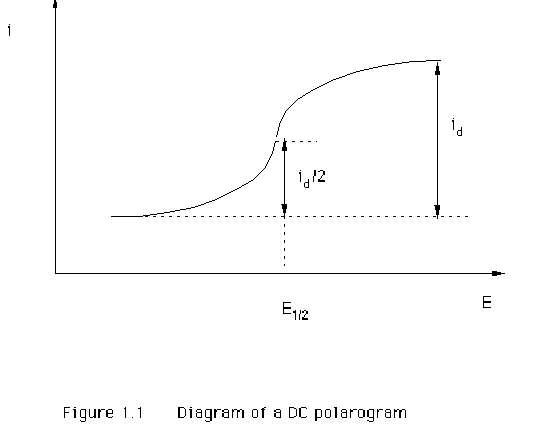
If an electroactive species is capable of undergoing a redox process at the DME, then an S-shaped current-potential relation is usually observed. This is called a polarographic wave. Figure 1.1 illustrates the response obtained from a reduction reaction where the current (i) increases over a particular potential (E) range until it reaches a limiting value. The limiting current is the diffusion-controlled limiting current (i_d). This i_d is of interest in analytical measurements as it is proportional to the concentration of reactant. Ilkovic [4] first put the measurement of this current on a theoretical basis, and his equation is [4-6]

i_d = (7/3)^1/2 (36 p)^1/6 r^2/3 nF D^1/2 m^2/3 t_d^1/6 C (2.1)

where r is the density of mercury, n is the number of electrons, F is Faraday's constant, D is the diffusion coefficient, m is the flow rate of mercury, t_d is the drop time, and C is the concentration of the electroactive species in the bulk solution.

For a planar electrode,

i_d = nFAD^1/2 C / (p t_d)^1/2 (2.2)

For a spherical electrode with radius r,

i_d = i_d(planar)+nFADC / r = nFAD^1/2 C (1/ (p t_d)^1/2 + D^1/2 / r) (2.3)

For a microelectrode, a steady-state current is

i_d = GnFA^1/2 DC (2.4)

where G is an electrode geometry constant, only depending on electrode geometry.

For a microdisc electrode, G=4/(p)^½

i_d =4/(p)^½nFA^1/2 DC = 4nFDC r

For a microsphere electrode, G=2p^½

i_d = 2p^½nFA^1/2 DC = 4pnFDC r

The half-wave potential E_1/2 is another important parameter of the DC polarogram. This is the potential at which the current reaches half of its limiting value (Figure 1.1). The value of half-wave potential is usually independent of concentration and is characteristic of the electroactive species. Therefore it can be used for qualitative characterization of the species, and is the foundation of qualitative analysis.

The shape of the DC polarogram is also very important to the overall characterization of the electrode process. If the reduction reaction is reversible and controlled by diffusion, the potential (E) is related to the concentrations of reactant and product by the Nernst equation [7]:

E = E° + (RT/nF) ln( C_O(0)/C_R(0) ) (2.5)

where E° is the standard redox potential, R is a gas constant, T is temperature, C_O(0) and C_R(0) are the surface concentrations of species Ox and Red, respectively. The shape of the DC polarographic wave is then derived by combining the Nernst and Ilkovic equations as follows [8, 9]

E = E_1/2 + (RT/nF) ln( (i_d- i)/i )

i = i_d / [1 + exp( (nF/RT) (E - E_1/2))] (2.6)

where

E_1/2 = E° + (RT/2nF) ln( D_R/D_O ) (2.7)

Since the diffusion coefficients of oxidized and reduced forms, D_O and D_R, are often almost equal, then E_1/2= E°. When i = i_d/2, then E = E_1/2.

Equation (2.6) is the Heyrovsky-Ilkovic equation, and is often used in investigations into the nature of electrode processes. However, an experimental DC polarogram also shows the oscillatory behavior of the current due to the growth and fall of the mercury drop, and this is superimposed on the DC behaviour. This invariably causes problems in the measurement of wave heights and/or half-wave potentials, and of course has deleterious effects on measures of analytical performance, especially sensitivity and resolution. Despite these problems, the DME remains popular because of its constantly renewed surface.

2.3 Linear Sweep Voltammetry and Cyclic Voltammetry

Linear sweep voltammetry (LSV) is performed by applying a linear potential ramp in the same manner as DCP. However, with LSV the potential scan rate is usually much faster than with DCP. When the reduction potential of the analyte is approached, the current begins to flow. The current increases in response to the increasing potential. However, as the reduction proceeds, a diffusion layer is formed and the rate of the electrode reduction becomes diffusion limited. At this point the current slowly declines. The result is the asymmetric peak-shaped I-E curve, as in Figure 1.3.

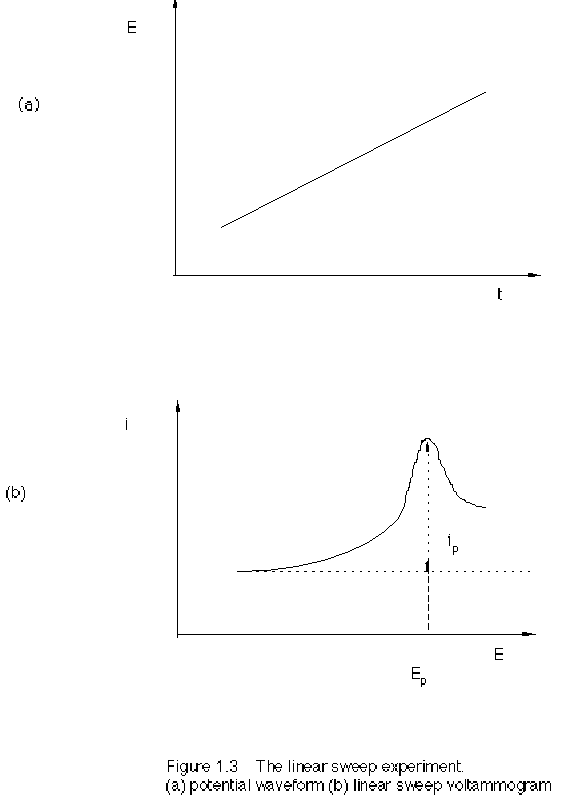
For a reversible reaction, the peak current is

I_p = 0.4463 nFAC (nFvD/(RT))^1/2 (2.8)

The peak potential is

E_p = E_1/2 – 1.109 RT/(nF) (2.9)

The half-peak potential is

E_p/2 = E_1/2 + 1.09 RT/(nF) (2.10)

The difference between peak potential and half-peak potential, similar to the half-peak width, is

| E_p - E_p/2 | = 2.2 RT/(nF) = 56.5/n (mV) at 25 °C (2.11)

Cyclic voltammetry is similar to linear sweep voltammetry except for the potential scans from the starting potential to the end potential, then reverse from the end potential back to the starting potential. The difference between two peak potentials is

DE_p =| E_pa - E_pc | = 2.3 RT/(nF) = 58/n (mV) at 25 °C (2.12)

For a non-reversible reaction, DE_p becomes larger.

2.4 Alternating Current Polarography

A number of modifications to DCP have improved its analytical performance. One of them is alternating current polarography (ACP). ACP is the result of superimposing a small amplitude sinusoidal potential (DE) with a fixed frequency (w) on a slowly scanning DC ramp, as (c) in Figure 1.2. The applied potential is then given by summing the AC and DC components. Finally, the alternating current (AC) is measured as a function of DC potential. In particular, the amplitude of the AC current vs. the DC potential is plotted, as (g) in Figure 1.2. The current-potential (I-E) curve for a reversible reaction follows the equation [6]

I = n²F² AC DE (wD)^1/2 sech² [(nF/2RT)(E - E_1/2)] /(4RT) (2.13)

At a peak, sech()=1, then the above equation reduces to

I_p = n²F² AC DE (wD)^1/2/(4RT) (2.14)

It may be deduced from this equation that the amplitude of the AC component of the Faradic current (I) is peak-shaped. Moreover, the peak current is a linear function of concentration and therefore may be used in analytical applications. Like the half-wave potential E_1/2 in DCP, the peak potential E_p in ACP is characteristic of the electroactive species. Also, the half-peak width (i.e. the width of the peak at half its height, W_1/2) is [6]

W_1/2 = 3.52 RT/(nF) = 90/n mV at 25 °C. (2.15)

2.5 Square Wave Polarography

Square wave polarography (SWP) uses a small amplitude square wave voltage in place of the sinusoidal one used in ACP. Its potential waveform is shown in (d) of Figure 1.2. The current is sampled near the end of each square wave half cycle, to minimize double-layer charging effects, and the I-E response is obtained by plotting the differences in current between successive half cycles. For reversible electrode processes, the I-E curve for SWP is similar to that in ACP [6], so its properties, including the half-peak width W_1/2 and resolution, are obviously akin to ACP.

2.6 Normal Pulse Polarography

The pulse polarographies including normal pulse polarography (NPP) and differential pulse polarography (DPP) stem from Barker's original work on square wave polarography [6]. The increased sensitivity of these techniques over DCP arises from their ability to discriminate against the charging current by measuring the total current after the charging current has decayed to values substantially less than the Faradic current.

The potential-time waveform used in NPP is presented as (a) in Figure 1.2. At the beginning of the potential sweep, the electrode is held at an initial potential where no Faradic current flows. Potential pulses of increasing amplitude are then applied to the electrode at regular intervals. The potential pulses are about 50 ms in duration and the current is measured at a time near the end of each pulse. A potential pulse is ended by a return to the initial potential and the drop is dislodged. The whole process is repeated except a few millivolts are added to the potential pulse in next cycle. A normal pulse polarogram is shown as (e) of Figure 1.2. The shape of the normal pulse polarogram is sigmoidal, looking similar to the shape of a DC polarogram, and indeed it can be described by a current-potential equation similar to that in DCP [6].

For a planar electrode,

i_d = nFAD^1/2 C / (p t_p)^1/2 (2.16)

For a spherical electrode with radius r,

i_d = i_d(planar)+nFADC / r = nFAD^1/2 C (1/ (p t_p)^1/2 + D^1/2 /r ) (2.17)

2.7 Differential Pulse Polarography

Normal pulse polarography gives improved sensitivity by avoiding most of the charging current by sampling the total current as late as possible after the application of each potential pulse. However, there still is the charging current to some extent. Another defect of NPP is poor resolution between neighbouring wave because of drawn-out sigmoidal I-E response. Differential pulse polarography (DPP) was designed to overcome these problems by arranging a charging current of smaller magnitude, and by producing a peak-shaped I-E curve.

The potential-time waveform used in DPP is shown as (b) of Figure 1.2. A voltage ramp is applied to the electrode as in the DCP, and a small amplitude potential pulse (DE) is added to the voltage towards the end of each drop's life. The currents are measured before applying the pulse and at the end of the pulse. When the difference between the two current samples is plotted as a function of the applied ramp voltage, a peak-shaped current response is shown as (f) in Figure 1.2.

The peak-shaped I-E curve allows polarographic responses in close proximity to each other to be more clearly resolved than in either DCP or NPP. The I-E curve for all values of the pulse amplitude is described by [6]

I = nFAC (D/ p t_p)^1/2 P (s²-1)/[(s+P)(1+Ps)] (2.18)

where

s = exp(nFDE/(2RT)) (2.19)

P = exp[(nF/(RT))(E - E_1/2 + DE/2)] (2.20)

At a peak, P=1, then the current equation reduces to

I_p = nFAC (D/ p t_p)^1/2 (s-1)/(1+s) (2.21)

E_p = E_1/2 - DE/2 (2.22)

The half-peak width is a very important parameter in resolution. The half-peak width W_1/2 is a function of the pulse amplitude as follows [6]

W_1/2 = 2RT/(nF) cosh^-1[2 + cosh(nFDE/(2RT))] (2.23)

For large values of |DE| (say |DE| > 200/n mV), W_1/2 approaches to |DE|, and for small values of |DE| (e.g. |DE| < 20/n mV), this equation reduces to equation (2.15).

Unfortunately, the above theoretical equations are derived by neglecting the DC effect in DPP, and although this is not a problem when the ratio of the drop time to the pulse time is larger than 50, the resulting distortion makes the theoretical treatment complicated, especially for a non-reversible reaction.

2.8 Pseudo-Derivative Normal Pulse Polarography

DPP is a very sensitive electroanalytical technique due to the effective discrimination against the charging current. However, DPP has two problems associated with the slowly increasing DC ramp. As the DC ramp progresses, filming may occur on the surface of the electrode if species form insoluble mercury compounds [6]. Since the characteristics of the electrode are changed by such a film, the current may not correspond to the simple theory. Another problem is that the theory itself is complicated by the effect of the DC ramp. NPP avoids these two problems. But the disadvantage of NPP is its poor resolution because of the sigmoidal wave. To overcome this shortcoming, NPP polarograms can be differentiated to produce peak-shaped responses, and thus combine the best features of both DPP and NPP while avoiding some of their limitations. This pseudo-derivative normal pulse polarography (PDNPP) nevertheless is not sensitive as DPP.

The potential-time waveform in PDNPP is as in NPP, but the current data of PDNPP are displayed in a difference mode. The current is subtracted from those for the following pulses, and the difference is plotted as a function of potential, as in DPP.

The theoretical treatment of PDNPP is simple and easy. The reversible current-potential equation is similar to that of DPP except for the DC term [6]. The half-peak width or resolution is akin to that of DPP.

2.9 Stripping Voltammetry

Stripping voltammetry involves three main steps: deposition (preconcentration), equilibration, and stripping. The first step is to concentrate the analyte from the dilute test solution into or onto the electrode at negative reduction (or positive oxidation) potentials, usually accompanied by stirring. The second step is to leave the solution to settle down. The third step is then to strip the preconcentrated analyte from the electrode back into the solution by using one of the polarographic techniques described above. A major advantage of this method is its extremely sensitivity. This is because the concentration of the analyte on the electrode is 100-1000 times greater than that in the starting solution [6].

<big>Chapter 3
Features

This software analytically and digitally simulates voltammograms (polarograms) on virtually any mechanism at 9 electrode geometries in above techniques, calculates their theoretical peak current and potential, retrieve parameters by curve fitting, and separate overlapped peaks and baseline. </big>

· Digital simulation
Flexible for any mechanism up to second-order chemical reaction. You can type your mechanism and chemical symbols. An implicit finite difference algorithm.

· Analytical simulation
No divergence problem in simulation. No overflow problem in simulation. Fast simulation.

· Over 5 techniques
Linear sweep, CV, DC, normal pulse, differential pulse, square wave voltammetries. Multi-cyclic voltammetry, cyclic normal pulse, cyclic differential pulse, cyclic square wave voltammetries.

· Surface concentration
It shows what happen each species in the electrode surface.

· Theoretical peak
You can compare your data with theoretical peak values to see if your experimental conditions reach theoretical limit or not.

· Simulating effect of noise, charge current, resistance, electrolyte, stripping time, stripping potential, convection, etc.

· Separating overlapped peaks
It manually and auto separates overlapped peaks into individuals, and extract real peak from voltammogram with noise and baseline. So you can exactly determine peaks.

· Preconcentration
You can change preconcentration conditions for stripping voltammetry.

· Pre-equilibration

· Curve fitting
It manually and auto fits the simulated voltammograms into experimental data, and extracts kinetic parameters from experimental data.

· Import and export data
You can export simulated data into your favor program (e.g. MS Excel). You can copy-n-paste the voltammogram into your document.

· Derivative, integral, semi-derivative, semi-integral
Semi-derivative is useful for CV. It can change a shape of reversible CV into symmetric peak so easy to determine peak.

· 9 electrode geometries
planar, spherical, semi-spherical, cylindrical, semi-cylindrical, band, microdisk, thin film, and rotating disk electrodes.

· Tip
It shows tip for help when you put mouse cursor over a label.

Table 1 Feature

Version	Shareware	Student	Standard	Full	Competitor
digital simulation	y	y	y	y	y
analytical simulation	y	y	y	y	n
theoretical peak	y	y	y	y	n
multi-electron reaction	y	y	y	y	n
surface concentration	y	y	y	y	n
any species symbol	y	y	y	y	n
tip	y	y	y	y	n
Import and export data	n	y	y	y	y
Techniques:
LSV and CV	y	y	y	y	y
DC	y	y	y	y	n
normal pulse	y	y	y	y	n
differential pulse	n	y	y	y	n
cyclic diff. pulse	n	y	y	y	n
square wave	n	y	y	y	n
Cyclic square wave	n	y	y	y	n
Effect:
convection	y	y	y	y
noise	y	y	y	y	y
charge current	y	y	y	y	y
resistance	y	y	y	y	y
electrolyte	y	y	y	y	n
preconcentration	y	y	y	y	n
pre-equilibration	y	y	y	y	y
Analysis:
differentiate	y	y	y	y	n
integrate	y	y	y	y	n
Semi-differentiate	y	y	y	y	n
Semi-integrate	y	y	y	y	n
manual fit	y	y	y	y
auto fit	n	n	y	y	y
manual separate	y	y	y	y	n
auto separate	n	n	n	y	n
Electrode:
planar	y	y	y	y	y
(micro)spherical	y	y	y	y	y
(micro)hemispherical	y	y	y	y	y
(micro)cylindrical	y	y	y	y	y
(micro)hemicylindrical	y	y	y	y
microdisc	y	y	y	y	n
band	y	y	y	y	n
thin film	y	y	y	y	n
rotating disc	y	y	y	y	n

Note: y = yes, n = no. Price may be changed.

<big>Chapter 4
Menu</big>

File menu

· Save submenu
It saves experimental parameters.

· Import Data submenu
It imports data from a file into Polar. The Plot window title will show the file name of data.

· Export Data submenu
It exports data to other program as data file. e.g. if you export data as the .csv file, you open it into MS Excel by double-clicking it.

· Copy To Clipboard
It copy graph into clipboard, so you can paste graph into your document.

· Print
It prints graph.

· Exit

Input menu

· Technique submenu

Select one of 5 techniques. The default technique is LSV and CV.

· Mechanism submenu

Input your mechanism and species symbol on Digital simulation, or choose predefined mechanism on Analytical simulation. The default mechanism is Fe³⁺ + e = Fe²⁺.

· Instrument submenu

Change instrument parameters. You can use the default values without any change.

· Chemicals submenu

Input chemicals parameters. You can use the default values without any change.

Run menu

· Simulate submenu
It runs simulation.

· Manual Fit submenu
It fits simulated curve into experimental curve as you manually change parameter values.

· Auto Fit submenu
It auto fits simulated curve into experimental curve.

· Manual Separate submenu
It separates overlapped peaks into individuals as you manually change parameter values.

· Auto Separate submenu
It auto separates overlapped peaks into individuals.

Display menu

· Option submenu
It is to change plot options.

· Plot submenu
It plots curve without run simulation.

· Next submenu
It plots next curve.

· Time

Display the simulation time and curve-fitting time.

· Clear submenu

Clear the Result window.

Analyze menu

· Find Peak submenu

Find the peak current and potential of curves of the peak shape.

· Find halfwave E submenu

Find the halfwave potential and limiting current of curves of the S shape.

· Theoretical Peak submenu

Calculate the theoretical limiting current, peak current and potential from theoretical equations. You select a mechanism from Analytical Simulation in the Mechanism window.

· Semi-differentiate submenu

Deconvolution.

· Semi-integrate submenu

Convolution.

· Differentiate submenu

· Integrate submenu

· X Data submenu

Multiply 10, 1000, 0.1, or 0.001 on X data. If your experimental potential data is not in Volt unit, you should convert to Volt unit by this submenu.

X data reverse submenu

Reverse the order of data.

· Y Data submenu

Multiply 10, 1000, 0.1, or 0.001 on Y data. . If your experimental current data is not in Amp unit, you should convert to Amp unit by this submenu.

Help menu

· Logon submenu
You logon to activate menus by input of password.

· Manual submenu
It displays this manual.

Some menus will be activated only after you click the Simulate submenu or load data because they require data.

<big>Chapter 5
Input</big>

5.1 Techniques window

1) Linear sweep and cyclic voltammetry
2) DC voltammetry
3) Normal pulse voltammetry and cyclic normal pulse voltammetry
4) Differential pulse voltammetry and cyclic differential pulse voltammetry
5) Square wave voltammetry and cyclic square wave voltammetry

The shapes of DC and normal pulse polarogram are S-shape. The shapes of differential pulse and square wave voltammograms usually are peak-shape. But there is effect of the DC term on differential pulse voltammogram.

5.2 Mechanism window

You can type in your mechanism in Digital Simulation section by any symbol. In order to faster computation, you should type in reactants only without products if chemical reaction is irreversible. In Analytical Simulation, you choose a predefined mechanism.

5.3 Instrument Window

Instrumental Parameters Section:

E start: starting potential (V).
E end: ending potential (V).
E step: step potential (V).
v: scan rate (V/s). For square wave voltammetry, v=E step/t pulse.
E pulse: pulse potential (V).
T: temperature (°C).
t pulse: pulse time or pulse width for pulse voltammetry (s).
t drop: mercury dropping time or pulse length in pulse voltammetry (s).
Noise: ratio of noise to maximum signal (%).

Scan:
Single: single scan.
Cycles: cyclic scan, e.g. cyclic voltammetry (CV).
2 Cycles: 2-cycle scan.

Electrode Section:

Planar: planar electrode.
(Micro)Spherical: spherical electrode or micro spherical electrode.
(Micro)Hemispherical: hemispherical electrode or micro hemispherical electrode.
(Micro)Cylindric: cylindrical electrode or micro cylindrical electrode.
Microdisc: microdisc electrode, radius <1e-4 cm.
Thin film: thin film electrode.
Rotating disc: rotating disc electrode with convection.
Area: electrode area (cm²). When you change the value of area, the value of radius is changed automatically.
Radius: electrode radius (cm). When you change the value of radius, the value of area is changed automatically.
Length: electrode length for cylindrical electrode or micro cylindrical electrode, or mercury film thickness for stripping voltammetry (cm).

Rotation: electrode rotation rate (rpm).

Preconcentration Section:

E pre: preconcentration potential (V).
R stir: stirring rate (rpm). Stirring solution.
t pre: preconcentration time (s).
t pre const: preconcentration time constant (/s).
P const: electrode constant. It only related to electrode.

Baseline section:

C dl: double layer capacitor for charge current (F).
R: resistance (Ohm).

I start: a starting current (A).

I end: an ending current (A).

5.4 Chemicals Window

Pre-equilibration option:

When this option is enabled, it automatically assumes that all the chemical and electrochemical reactions in the vicinity of the electrode surface are in equilibrium as determined by the thermodynamic parameters: chemical equilibrium constant Keq, the standard potential E°, and by the starting electrode potential E_start. Then, the entered values of analytical concentrations are not identical to the corresponding initial concentrations.

It is a good idea to keep the pre-equilibration option enabled. When the pre-equilibrated and analytical concentrations are different significantly, the initial condition for the experiment and the simulation may not be what was expected. The degree, to which the pre-equilibrated concentrations may be considered to be the bulk concentrations, will depend upon time of pre-equilibration (i.e., the time between setting the starting potential and initiating the potential scan), the operative kinetics, and the geometry. The value of the initial concentrations will act as if they are the bulk concentrations. A reasonable assumption only if the electrode geometry does not produce steady-state diffusion and if the pre-equilibration time is much longer than the duration of experiment.

When the pre-equilibration is not selected, the pre-equilibrated and analytical concentrations are the same.

Species Section:

D: diffusion coefficient (cm²/s).
C anal: analytical concentration (M).
C init: initial concentration for simulation (M).
C fitted: fitted value of concentration (M).
C min: minimum concentration for fitting (M).
C max: maximum concentration for fitting (M).

Heterogeneous Reaction Section:

ks: heterogeneous standard rate constant (cm/s).
a: electron transfer coefficient.
n: electron number.
E°: standard electrode potential (V).

Homogeneous Reaction Section:

kf: forward chemical reaction rate constant.
kb: backward chemical reaction rate constant.
Keq: chemical equilibrium constant, Keq = k_f/ k_b.

<big>Chapter 6
Playing Around</big>

6.1 Running Simulation

A simplest way to run simulation is just to click the Run menu and then the Simulate submenu. It uses the default values to simulate a linear sweep voltammogram. You can change chemical parameters in the Chemical window under the Chemical menu, or change instrumental parameters in the Instrument windows under the Instrument menu, or change mechanism in the Mechanism window under the Mechanism menu.

Notice that some menu (e.g. the Display menu and the Analysis menu) will be activated only after run simulation or load data because they require data.

6.1.1 Effect of Electron Number

Change the electron number of charge reactions in Digital Simulation section for both Digital and Analytical Simulation. Peak height increases and peak width decreases as the electron number increases.

6.1.2 Effect of Electrode Geometry

Simulation technology for microelectrode is the same as for macro electrode, but the electrode size is very small, e.g. electrode radius is 1e-4 cm. A shape of linear scan voltammogram at spherical electrode is changed from peak shape to S-shape. When the products of scan rate and radius, vr > 10^-5, the shape is peak. When vr < 10^-7, the shape is wave. Note that the planar electrode geometry is not available for microelectrode.

The rotating disc electrode is similar to spherical electrode. When the ratio of rotating speed to scan rate, w/v < 1, the shape is peak. When w/v > 10³, the shape is wave.

6.2 Comparing Curves

After run first simulation, click the Display menu, and then the Option submenu. Select the Overlap choice, and then run second simulation.

6.3 Analyzing Data

Semi-derivative is useful for CV. It can change a shape of CV into symmetric peak for easy measurement.

6.4 Calculating Theoretical Limiting Current

Click the Analyze menu and then the Theoretical Peak submenu to calculate the values of theoretical limiting current, peak current and potential. Change a mechanism for the theoretical peak from the Analytical Simulation section in the Mechanism window.

6.5 Extracting Parameters by Curve Fitting

6.5.1 Fitting to Simulation Curve

In order to extract kinetic parameters, you can fit a simulation curve to another simulated or experimental curve. It can retrieve any of 30 parameters (eg. concentration C, standard electrode potential E°, and the heterogeneous standard rate constant ks) from voltammogram by curve fitting. You select a parameter that you want to fit, input the minimum and maximum values of the parameter. e.g. after run simulation with all default values, select a concentration, then change the C value from 1e-3 to 2e-3 in the Species section, click the Auto Fit menu. You will see the fitted value of 0.001 in the C fitted field next to the C text field.

You should manual fit before auto fit. The manual fit shows how well your initial guesses values work. . If it diverged, you should change their initial values, then try again.

6.5.2 Fitting to Experimental Curve

It is similar to fit simulated curve. But you should input your experimental values of E_start, E_end, E_step, etc. into the Experimental section. Polar requires that data are in SI unit and first peak is positive value. If your experimental data are not, please convert your experimental data. E.g. click the Analyze menu, and then the 0.001Y submenu to convert current from mA to A.

6.6 Stripping Voltammetry

Select the Preconcentration in the Experiential Parameters window. Change the preconcentration potential value in the E pre text field, and preconcentration time in the t pre text field. The preconcentration potential value usually is -0.2/n V to specie’s standard electrode potential. The preconcentration time usually is a number of minutes. You should enter your electrode constant into the P cont text field, and your mercury film thickness into the Length field in the Electrode section of the Experimental window if you use a planar mercury film electrode.

<big></big>Chapter 7
Frequently Asked Questions (FAQ)

Q: Which platforms can Polar run on?
A: Its 32-bit version Polar runs on IBM PC under Windows 95/98/NT while its 16-bit version Polar runs under Windows 3/3.1/3.11/95/98/NT.

The 32-bit version needs Microsoft Visual Basic 6 runtime DLL files (e.g. msvbvm60.dll, comdlg32.ocx) in the same directory as Polar or in the directory \windows\system for Windows 3.11 or 95, or in the directory \winnt\system32 for Windows NT.

The 16-bit version needs Microsoft Visual Basic 4 runtime DLL files (e.g. vb40016.dll and oc25.dll) in the same directory as Polar or in the directory \windows\system for Windows 3.1, or in the directory \winnt\system for Windows NT.

Q: I cannot save a file.

A: You miss the Microsoft Visual Basic 6 runtime DLL file comdlg32.ocx.

Q: Where can I download these dll?

A: Microsoft Visual Basic 6 runtime DLL files are from http://www.simtel.net/simtel.net/win95/dll.html, where msvbvm60.dll is inside simvb6-5.zip. Microsoft Visual Basic 4 16-bit runtime DLL files are from http://www.simtel.net/simtel.net/win3/dll.html.

Q: When I click the Simulate menu, I got error: “No data”, or "Run-time error 13”, with the message: "Type mismatch".

A: I guess you are running it under non-English version of Windows. Please change language setting to English in the Regional Setting of the Control Panel, and restart Polar. Or try it under English version of Windows. Some non-English versions of Windows have problem to run English version program.

Q: When I installed to run setup.exe, an error occurred:
while registering the file
>c:\windows\system\MSRD2x35.dll
Shall I (Abort, Retry, Ignore)?
A: Ignore. Do not worry about MSRD2x35.dll. Running Polar did not use it, setup.exe check it only.

Q: Still have install problem?
A: You should close all programs (include Office, Mail) before install Polar. If you still have problem, try to register file msvbvm60.dll by double click or type following command in DOS:

Cd \windows\system
Regsvr32 msvbvm60.dll
then start Polar.

Q: Why are some menus inactive?
A: Some menus will be activated only after you click the Simulate menu or load data because they need data.

Q: I cannot see any chemical reaction in Public version. Is this part of the program not finished yet or is it only available in the registered version?
A: There is only one chemical reaction available in the Public version. You can change chemical reaction rate kf, e.g. 10¹⁰. The registered versions simulate virtual any mechanisms.

Q: Does it include my mechanism?
A: If your mechanism is missing, please send your requirement into author. Author may add your mechanism into new version special for you.

Q: Can it fit data by curve fitting?
A: Yes. Click to select a parameter that you want to fit, and then click the Auto Fit menu.

Q: Can I change graph into other program Lotus 123 or Excel?
A: Yes. You export data in text file, and then read data into Lotus 123 or Excel.

Q: Some submenus semi-derivative, semi-integral, derivative, and integral, seem to not work sometime. How can I do?
A: You should first click the Next submenu under the Plot menu, then try semi-derivative submenu.

Q: How much does registration cost?
A: About $100.

Q: How can I get registered version?
A: You will receive it if you send author register fee by check or money order.

Q: What are differences among Shareware, Standard and Professional, and Full versions?
A: The Shareware version is for teaching, the Standard version is for average users, the Professional version is for professionals, and the Full version is for special users.

Q: When I run the SWV with default conditions as a digital simulation, it does not appear to give the correct curve. Why?
Because default conditions are for linear sweep and CV only. For SWV, DC, NPV and DPV, you should change scan rate v to 0.01. For SWV you should calculate correct scan rate by v=E step/t pulse before run digital simulation.

Q: Is it possible to click on a point and then have displayed both the current and potential for the point? Also, does it have any zoom features?
A: You can import any ASCII x-y data from Polar to my software VisualMath For Java. In VisualMath For Java, you click on a point and then have displayed both the current and potential for the point. Also, it has zoom features.

Q: How to simulate oxidation reaction?

A: change the E_start < the E_end in the Instrument window.

Q: How does it compare to competitors?
A: Polar has advantages over competitors:

1. Competitor simulates a single technique CV only; while Polar has more features, e.g. Polar simulates over 5 techniques (see details on the table in Chapter 2 Features).

2. Competitor cannot separate overlapped peaks, while Polar does.

3. Competitor does not support Windows 95 features, e.g. long filename, while Polar does.

4. Competitor cannot simulate multi-electron reaction in one step, while Polar does.

5. You download and try Polar free.

6. Polar is much cheaper.

7. You do not worry about if you lose the Dongle. Competitor is copy-protected by the Dongle, but Polar is not.

<big>Chapter 8
References</big>

[1] W. Huang, T. Henderson, A.M. Bond and K.B. Oldham, Curve fitting to resolve overlapping voltammetric peaks: model and examples, Anal. Chim. Acta, 1995, 304, 1-15.

[2] W. Huang and B. Hibbert, Computers & Chem., 1995, 19(4), 433.

[3] W. Huang and B. Hibbert, Computers & Chem., 1995, 19(4), 435.

[4] W. Huang and B. Hibbert, Polar 2.0 for Windows: simulator of voltammogram, Chem. in Aus., 1996, 131.

[5] J. Mo, P. Cai, W. Huang and F. Yun, Theory and application on multiple semidifferential electrochemical stripping analysis with thin mercury film formed in situ, Acta Chimica Sinica, 1984, 42(6), 556-561, [CA 101: 162712].

[6] A. J. Bard and L. R. Faulkner, Electrochemical Methods, John Wiley & Sons, New York, 1980.

Contents

<big>Chapter 1 Introduction</big>

<big>Chapter 2

Polarography and Voltammetry </big>

<big>Chapter 3 Features

<big>Chapter 4 Menu</big>

<big>Chapter 5 Input</big>

<big>Chapter 6 Playing Around</big>