Computer representation of chemical bonds

To show the molecule on the computer screen, the computer must be told about molecular structure. Molecular modeling software requires that this information be provided in the form of a sketch on the screen which is usually done with a mouse or some other pointing device, or prompts the user for a name of the disk file where the information is stored. This section discusses examples of different ways in which the chemist's drawing of a molecule may be converted into a series of numbers which computer understands.

Each atom of the molecule is usually assigned an ordinal number, from 1 to N, where N is the total number of atoms in a molecule. Most modeling systems do not impose a particular atom numbering, hence the atom numbers usually do not adhere to strict rules of IUPAC convention. However most modeling systems require that atoms belonging to a given residue (e.g. amino acid in a protein) be numbered consecutively.

Usually, the atoms comprising the molecule are assigned a type which describes their chemical identity. This type is usually an integral number or a mnemonic symbol, e.g.: ``21'' or ``Csp3''. The type reflects not only an element but also a particular arrangement of bonds formed by the atom, and its formal charge. The atom type may also depend on atom neighbors in the molecule. For example, the amine, ammonium, imine, amidic, pyridinic, pyrrolic, etc., nitrogens are assigned different types in most molecular modeling systems. There is still no universal table of atom types because different approaches may require different levels of detail in atom type specification. Similarly, bonds are assigned types: single, double, aromatic, hydrogen, etc. Besides real chemical atoms and bonds, most systems introduce the notion of a dummy atom and dummy bond (the terms virtual or pseudo are also frequently used). These objects can be used in marking important features of the molecule, for orienting two molecules relative to each another, or enforcing some geometrical constraints on real atoms and bonds of the molecule.

The relation between atoms must be given to completely specify molecular objects to the computer. This information consists of two parts: the specification of bonds and specification of geometry (the spatial relation between atoms). With millions of known molecules, it is surprising to discover that there is still no accepted standard for representing molecular structure.

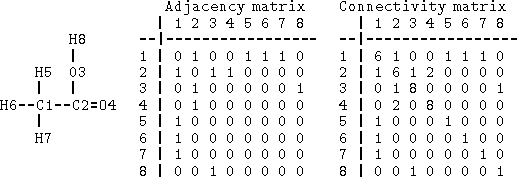
Figure 6.1: Adjacency and connectivity matrices for acetic acid. Rows and columns correspond to the atom numbering given on the left. Off-diagonal elements of both matrices represent order of the bonds between atoms pointed by row and column. The diagonal of the connectivity matrix represents the atomic number.

Bonds can be specified as a list of bonded atom pairs accompanied by bond types or as an adjacency matrix or attachment list. The example of an adjacency matrix is shown in Fig. 6.1. It is a square matrix with the number of columns and rows equal to the number of atoms in the molecule. Positions corresponding to bonded atoms are marked with 1 (or sometimes by bond type), and all other entries are zero. A variant of the adjacency matrix, called connectivity matrix, differs in that it includes the atomic number on the diagonal and for each bond the actual bond order (i.e., 1 for single bond, 2, for double, 1.5 for conjugated, etc.) is used. The attachment list is constructed by listing all atoms bonded to a given atom. An example of an attachment list for acetic acid is given in Fig. 6.2.

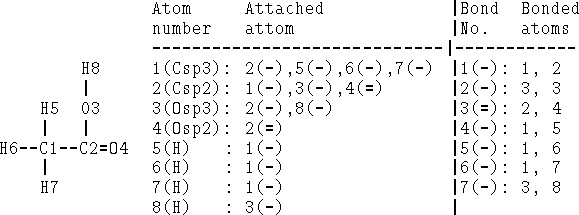
Figure 6.2: Attachment list and bonded atom list for acetic acid as depicted on the left. Single bonds are denoted as (-) and double as (=).

Many computer operations on molecules are based on principles of graph theory (topology). Software manuals and research papers frequently use terms and concepts of the graph theory. Some basic definitions will be given below, however do not be mislead by the simplicity of concepts explained in the next few paragraphs. The graph theory is an active, important and difficult branch of mathematics. It also has many important practical applications in fields as diverse as electronics and cartography. For a recent review of the application of graph theory to molecular modeling consult Marsili, (1990).

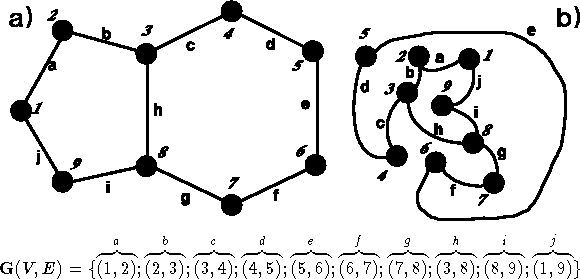
Figure 6.3: Two isomorphic graphs.

A graph, such as tex2html_wrap_inline1918 in Fig. 6.3, is a collection of points, V (most frequently called vertices or nodes), and lines, E (commonly called edges but the term bonds is also used). Graphs are frequently specified as a list of edges (see Fig. 6.3). The valence (or degree) of a vertex is the number of edges originating from this vertex. The sum of degrees of all vertices is even and equal to twice the number of edges. This fundamental property of graphs is called a handshaking lemma. Two vertices are called adjacent if they are joined by an edge. Similarly, two edges are adjacent when they originate at the same vertex. Fig. 6.3a represents a graph which some may consider similar to a molecule. Note, however, that ordinary graphs do not assign any spatial arrangement to the vertices. Edges can be any length, and the graphs which you see depicted in Fig. 6.3a and 6.3b are identical. Graphs representing molecules belong to a class of undirected graphs, i.e., graphs with edges not directed from one vertex to another (edge (i,j) is equivalent to (j,i)). Two graphs are isomorphic if one can convert the first graph to the second one by renumbering vertices. The efficient algorithms for detecting isomorphism are actively researched due to their importance for fast computer searching of chemical databases. The problem is far from trivial, since the number of ways in which the graph vertices can be numbered, tex2html_wrap_inline1928 , is astronomical even for small molecules.

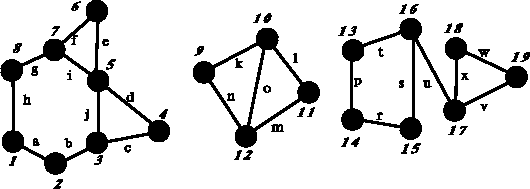
Figure 6.4: Example of disconnected graph with circuits. This graph contains three components (1--8, 9--12 and 13--19) and seven independent circuits.

Some sequences of edges have special names. The ``walk'' is such a sequence of edges where consecutive edges are adjacent. The ``trail'' is a walk in which each edge is traversed only once. The ``path'' is a trail in which all vertices are visited only once, with the exception that the first and last vertex may be identical, in which case the path is closed. Closed paths are also called ``circuits''. Using as an example a graph in Fig. 6.4, the sequence of edges: a tex2html_wrap_inline1930 b c d j c d is a walk. The walk: j e f i d c is a trail, but is not a path since vertex 5 was crossed twice, however, the walk: r s u v is a path. A graph is connected when there is a path between any pair of vertices. Please note that the two strands of DNA in a double helix, are usually considered separate components since hydrogen bonds are not routinely included as edges in the molecular description. The number of components of the graphs is the number of disjointed sets of vertices between which there is no path. The graph in Fig. 6.4 has 3 components, but the removal of edge u would produce a graph with 4 components. All edges whose removal disconnects the graph are called a disconnecting set.

Figure 6.5: Example of a graph with circuits (right) and its spanning tree (left).

A connected graph without a circuit is called a tree. The tree has several important properties:

removal of any edge disconnects the tree (i.e., all edges belong to a disconnecting set),
there is one and only one path between any two given vertices, and
if n is the number of vertices in a tree and m is the number of edges then m = n - 1.

It is easy to see that if a molecule is a tree, all its bond lengths and angles are independent of each another. One can change any of them without affecting the other. If a molecule contains circuits (which chemists call rings or cycles) only the lengths and angles associated with bonds belonging to the disconnecting set can be changed without affecting other bonds and angles. For molecules containing rings, it is desirable to find a spanning tree (see Fig. 6.5) of their graph by removing one edge for every circuit (note that the number of vertices is not affected by this operation). Such a spanning tree must be found if one needs to change a length or an angle involving a bond which is a part of a ring system. This change will always affect angles and lengths associated with bonds which were removed to obtain a spanning tree. There is an important relation which is often used in molecular modeling systems to check the consistency of the molecular object. If n, m, r, and k denote the number of vertices, edges, circuits, and components, respectively, then: r = m - n + k. Check this relation by using Fig. 6.4 as an example. Please note however, that r refers here to the number of smallest circuits. To find the number of smallest circuits, one starts by marking all circuits of size 3, then 4, 5, etc., but counts only those circuits for which there is at least one edge, which was not previously incorporated into a smaller circuit. The process is continued until all edges belonging to rings were used up. For the graph in Fig. 6.4, the closed paths: l tex2html_wrap_inline1930 m o and k n o are counted as distincts circuits, while the path: k l m n is not considered a distinct circuit, since all its edges were already included in smaller circuits.

The algorithms derived from graph theory are used extensively in molecular modeling software. Even for simple operations, like modifying bond lengths or angles, the topological methods must be used in order to see if a bond is part of a ring system, since only bonds belonging to a disconnecting set may be independently modified. Assigning atom types, detecting aromaticity and checking if the valence of atoms is satisfied requires that the topology of the molecule be analyzed. Topological concepts are used in the calculation of internal coordinates, performing conformational searches and converting standard chemical notation to representations of bonding suitable for computer analysis. We will see some examples in the following sections.

Next: Computer representation of geometry Up: Molecular Modeling Previous: Introduction

Computational Chemistry
Wed Dec 4 17:47:07 EST 1996

[ CCL Home Page ]
[ About CCL ] [ Resources ] [ Search CCL ] [ Announcements ] [ Links ] [ E-mail us ]
[ Raw Version of this page ]

Modified: Sat May 23 16:00:00 1998 GMT

Page accessed 11273 times since Mon Apr 19 14:12:13 1999 GMT