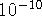 m. Also,
atomic units are frequently used: 1 a.u. = 1 Bohr = 0.529177249 Å.
m. Also,
atomic units are frequently used: 1 a.u. = 1 Bohr = 0.529177249 Å.
Molecules are not static entities. Even at absolute zero temperature
atoms in a molecule are actively vibrating. The molecular geometry
represented by a static picture on the computer screen or a Dreiding model
is therefore only an approximation. The term atom position is usually
understood as a position of the atom nucleus, or rather as some kind of average
position of the vibrating nucleus.
Luckily, the dimensions of an atom
nucleus are negligible compared to average bond lengths, and since
its mass is thousands of times larger than the mass of surrounding electrons,
the nucleus is the true center of gravity of an atom. The major conceptual
difficulty
is to decide what is an average position of a nucleus. Nuclear vibrations are
anharmonic, and hence,
the time average position of a nucleus is not located half
way between its extreme positions. Moreover, in molecules containing more
than two atoms, nuclei vibrate not only along chemical bonds but also
in directions perpendicular to them. That is why, depending on the method used
to interpret experimental results, slightly different values of bond
lengths and angles may be calculated.
Also, different
experimental methods measure different physical quantities. For example,
X-ray crystallography measures relations between ``electron clouds'' of
atoms,
while electron diffraction or neutron diffraction are based on scattering
from atomic nuclei.
Especially for hydrogen atoms, the nucleus is not located in the center
of the ``atomic cloud'' surrounding the proton. Bonds involving
hydrogen are substantially polarized and X-ray measurements will
underestimate them by as much as few tenths of an Ångström.
In other cases the differences are not as drastic, but one needs
to understand their origin in order to make the best use of experimentally
derived geometries. As you can see, ``molecular geometry'' may mean
different things depending upon the way in which it was derived or
measured.
Interatomic distances
are usually expressed in Ångströms, since distances between chemically
bonded atoms are of the order of 1 Å= 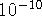 m. Also,
atomic units are frequently used: 1 a.u. = 1 Bohr = 0.529177249 Å.
m. Also,
atomic units are frequently used: 1 a.u. = 1 Bohr = 0.529177249 Å.
The simplest way to specify molecular geometry to the computer is to list cartesian coordinates for each atom. In most cases the right-handed coordinate system is used, whose axes are perpendicular to each other (i.e., orthogonal), as represented in Fig. 6.6.
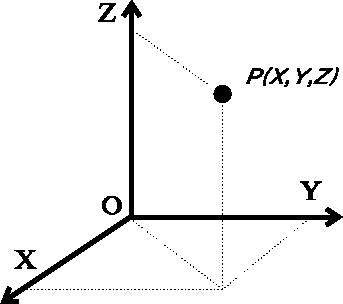
Figure 6.6: Cartesian system of coordinates with orthogonal axes.
Cartesian coordinates are usually listed in 3-column format, X, Y, and
Z coordinates for each atom. Sometime the coordinates are listed
in natural crystal axes, called notional axes, which refer to the shape
and dimensions of the unit cell.
The notional axes are not generally perpendicular,
and the coordinates are
scaled by lengths of the unit cell edges. For the general case
of a triclinic system,
represented in Fig. 6.7, the edges of the unit cell
along oblique axes, x, y and z,
are a, b and c, respectively, and the interaxial angles:
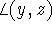 ,
, 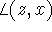 and
and 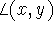 , are denoted by
, are denoted by
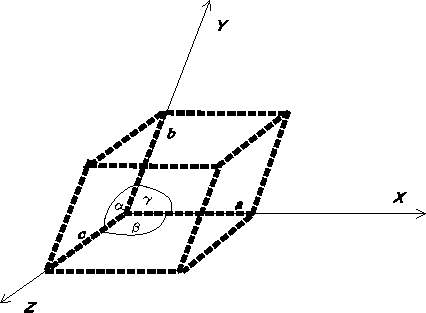
Figure 6.7: The unit cell with oblique axes for a triclinic crystallographic
system
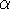 ,
, 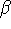 and
and 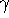 , respectively.
The coordinates expressed
in such a system can be transformed to the orthogonal cartesian
coordinates in several ways depending on the chosen orientation
of the oblique system with respect to the cartesian system. One such formula,
converting notional coordinates (x, y, z) to cartesian coordinates
(x', y', z') is given below:
, respectively.
The coordinates expressed
in such a system can be transformed to the orthogonal cartesian
coordinates in several ways depending on the chosen orientation
of the oblique system with respect to the cartesian system. One such formula,
converting notional coordinates (x, y, z) to cartesian coordinates
(x', y', z') is given below:
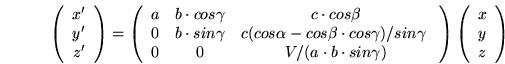 (6.1)
(6.1)
NOTE: There was an error in the original text and the formula was given as:
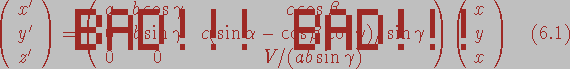 .
.
Thanks to Egon Willighagen (egonw@sci.kun.nl) and
Geoff Hutchison (hutchisn@chem.northwestern.edu) it was corrected
on 2002.04.18.
where
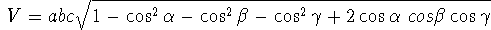
Cartesian coordinates are an efficient representation of molecular geometry for the computer, and have the advantage of including actual spatial orientation of the molecule. However, they lack the chemical contents for chemists. Chemists prefer to specify and analyze molecular geometry in terms of internal coordinates, i.e., bond lengths and bond angles. The most popular internal coordinates are shown in Fig. 6.10, but before explaining how values of internal coordinates are calculated from cartesian coordinates of atoms, it is necessary to explain some of the simplest operations on vectors. The reader is encouraged to refer to the college calculus books for the review of vector analysis.
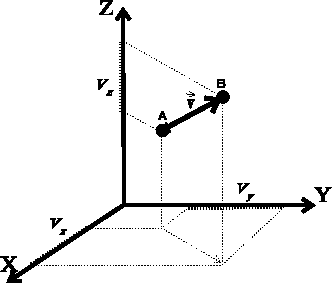
Figure 6.8: Definition of vector in cartesian coordinate system.
A scalar quantity is just a number, e.g., molecular weight.
A vector 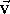 can be imagined as an
arrow starting
at some point A and ending at some point B. It is important to realize
that a vector is not in any way ``attached'' to points A and B, it merely
represents a direction from point A to B and a distance
between these points. If you translated
can be imagined as an
arrow starting
at some point A and ending at some point B. It is important to realize
that a vector is not in any way ``attached'' to points A and B, it merely
represents a direction from point A to B and a distance
between these points. If you translated the points to some other place,
the vector between them would still remain the same. The vector is given by its
3 components, i.e., the lengths of its projections onto each of the three
axes of the cartesian coordinate
system (see Fig. 6.8),
the points to some other place,
the vector between them would still remain the same. The vector is given by its
3 components, i.e., the lengths of its projections onto each of the three
axes of the cartesian coordinate
system (see Fig. 6.8), 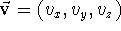 .
The components,
.
The components, 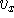 ,
, 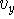 ,
, 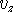 are scalars, however, their sign
depends on the direction of the vector. If the projection of the
vector on the given axis points in the positive direction of the axis, the
component is positive, otherwise, the component is negative.
Two vectors are equal if their components are equal. If a vector is given
by two points, its components are easily computed as differences between
corresponding coordinates of the vector end (``head'') and the
vector beginning (``tail''). In our case:
are scalars, however, their sign
depends on the direction of the vector. If the projection of the
vector on the given axis points in the positive direction of the axis, the
component is positive, otherwise, the component is negative.
Two vectors are equal if their components are equal. If a vector is given
by two points, its components are easily computed as differences between
corresponding coordinates of the vector end (``head'') and the
vector beginning (``tail''). In our case:
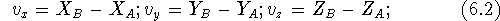
The length of a vector is the distance between its beginning and its end.
It is always positive (or zero, if the beginning and the end of a vector
are in the same place). Formally, the vector
length v (frequently written also as
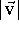 ) is given as the square root of the
sum of the squares of its components:
) is given as the square root of the
sum of the squares of its components:
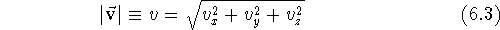
As with scalars (i.e., ordinary numbers), certain operations are defined for vectors. Adding two vectors means forming a new vector whose components are the sums of the respective components of the vectors being added:
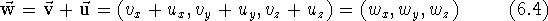
Subtracting two vectors is analogous, only here the components are subtracted. You can multiply vector by a scalar by multiplying each of its components by the scalar:
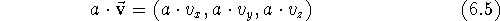
Similarly, dividing a vector by a scalar results in a vector whose components are divided by this scalar, however, you obviously cannot divide by zero. Multiplying/dividing a vector by a scalar results in multiplying/dividing its length by this scalar, while preserving its direction. The unit vector is a vector whose length is equal to 1. You may obtain the unit vector from any vector by dividing it by its own length. Such an operation is called normalization of the vector and is usually denoted as:
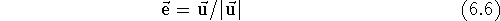
Note that adding a scalar to a vector does not make any sense and is not among the defined operations.
There are two different modes for multiplying a vector by another vector. The scalar product of two vectors, also called the dot product, results in a scalar. It is the product of the vector lengths multiplied by the value of the cosine of the angle between them. It can also be calculated as the sum of the products of corresponding components:
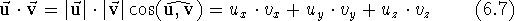
The dot product of two unit vectors is equal to the cosine of the angle
between them. Hence, the cosine of an angle formed by two vectors is
usually found by first normalizing the vectors and then calculating
their dot product(by summing up the products of their components). Note also
that the dot product does not depend upon the order in which the vectors are
multiplied (i.e.  ).
).
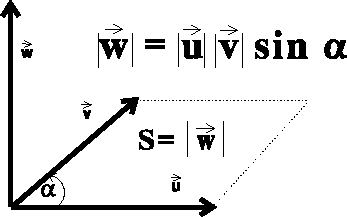
Figure 6.9: Vector product of two vectors.
The vector product of two vectors 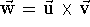 ,
also called the cross product, results in a new vector.
This vector is perpendicular to the
plane in which the multiplied vectors lie, and points in the direction given
by the right-hand screw rule (see Fig. 6.9).
The order in which the vectors are multiplied is important,
changing the order reverts the direction of the resulting vector.
The length of the resulting vector
,
also called the cross product, results in a new vector.
This vector is perpendicular to the
plane in which the multiplied vectors lie, and points in the direction given
by the right-hand screw rule (see Fig. 6.9).
The order in which the vectors are multiplied is important,
changing the order reverts the direction of the resulting vector.
The length of the resulting vector 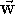 is equal in value
to the area of the parallelogram
constructed on the multilied vectors, i.e.:
is equal in value
to the area of the parallelogram
constructed on the multilied vectors, i.e.:
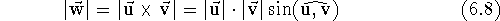
Alternatively, the components of the resulting vector 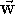 are
related to
the components of vectors
are
related to
the components of vectors  and
and 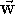 in the following way:
in the following way:
where the 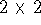 determinant is defined as:
determinant is defined as:
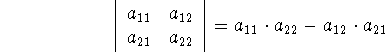
You may frequently see the term base vectors, written as:  ,
,
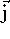 and
and 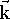 . These are unit vectors pointing
along positive directions of x, y and z axes of the cartesian
coordinate system. Note the simple relations between these vectors:
. These are unit vectors pointing
along positive directions of x, y and z axes of the cartesian
coordinate system. Note the simple relations between these vectors:
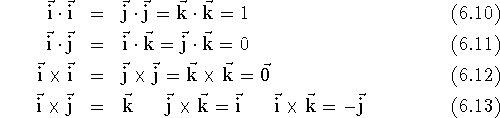
and  denotes
a zero vector, i.e., vector whose all components are zero.
denotes
a zero vector, i.e., vector whose all components are zero.
Internal coordinates are efficiently calculated by
the computer
from cartesian coordinates using the vector operations described above.
The bond length , 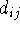 (Fig. 6.10a), is simply a distance between
two bonded atoms i and j, i.e., the length of the vector between atom i
and j:
(Fig. 6.10a), is simply a distance between
two bonded atoms i and j, i.e., the length of the vector between atom i
and j:
The valence angle called also bond
angle, 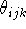 (Fig. 6.10b), between
bonds originating on atom j is calculated easily from the dot product of
vectors
(Fig. 6.10b), between
bonds originating on atom j is calculated easily from the dot product of
vectors 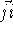 and
and 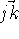 . However, the cosine rule can also be
used:
. However, the cosine rule can also be
used:
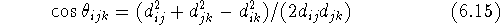
The valence angle is always positive and not larger than 180  , i.e.,
it is the smaller of the two possible angles.
, i.e.,
it is the smaller of the two possible angles.
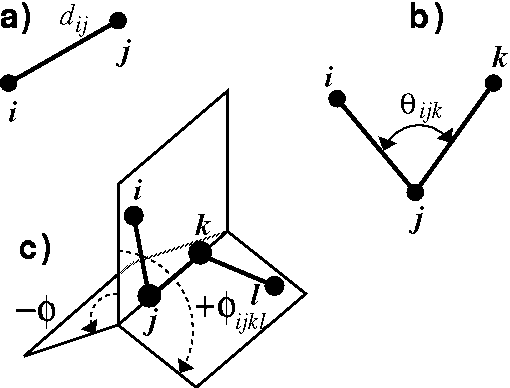
Figure: Internal coordinates: a) bond length, b) valence angle, c) torsional
angle.
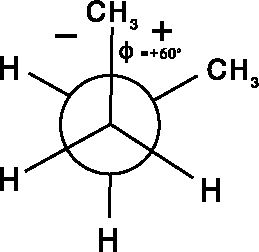
Figure 6.11: Newman projection of the 60  torsional
angle for central C--C bond in butane.
torsional
angle for central C--C bond in butane.
The torsional angle (Fig. 6.10c), is a dihedral angle, 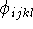 ,
between two planes passing through atoms i,j,k and j,k,l,
respectively. It is an angle between vectors normal (i.e., perpendicular)
to these planes, or
alternatively, an angle between the lines drawn on these planes
perpendicularly to the edge where planes intersect. In contrast to the
valence angle, the torsional angle
spans the range
,
between two planes passing through atoms i,j,k and j,k,l,
respectively. It is an angle between vectors normal (i.e., perpendicular)
to these planes, or
alternatively, an angle between the lines drawn on these planes
perpendicularly to the edge where planes intersect. In contrast to the
valence angle, the torsional angle
spans the range 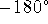 to
to 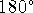 , i.e., the full revolution.
Its magnitude can be calculated as:
, i.e., the full revolution.
Its magnitude can be calculated as:
where 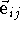 is a unit vector pointing from atom i to j.
Only the absolute value of the torsional angle can be derived by
eq. 6.16.
Additional checking has to be done to obtain the sign of the angle.
Unfortunately two opposing conventions are used for the sign
of a torsional angle.
The chemists use the right-hand screw rule, as indicated by the arrows in
Fig. 6.10c. In this case (assuming that we are looking along
the direction j -- k and our eye is on the side of j)
the clockwise turn from atom i to l,
with j and k being the pivots, represents
the positive angle while counterclockwise corresponds to negative values.
Mathematicians, however, use an opposing rule in which the sign of the angle
is positive for counterclockwise turns. Some modeling systems use this second
convention and you should be aware of it.
The torsional angles are frequently depicted as Newman projections as
illustrated in Fig. 6.11 for butane.
is a unit vector pointing from atom i to j.
Only the absolute value of the torsional angle can be derived by
eq. 6.16.
Additional checking has to be done to obtain the sign of the angle.
Unfortunately two opposing conventions are used for the sign
of a torsional angle.
The chemists use the right-hand screw rule, as indicated by the arrows in
Fig. 6.10c. In this case (assuming that we are looking along
the direction j -- k and our eye is on the side of j)
the clockwise turn from atom i to l,
with j and k being the pivots, represents
the positive angle while counterclockwise corresponds to negative values.
Mathematicians, however, use an opposing rule in which the sign of the angle
is positive for counterclockwise turns. Some modeling systems use this second
convention and you should be aware of it.
The torsional angles are frequently depicted as Newman projections as
illustrated in Fig. 6.11 for butane.
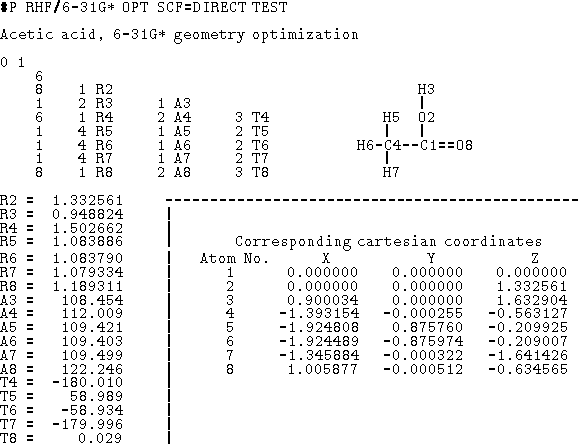
Figure 6.12: Data for Gaussian 90 program in the form of a
Z-matrix (cartesian coordinates included for reference). The first column
of the Z-matrix corresponds to atomic number. The next columns represent
atom numbers and internal coordinates (Rx -- distance, Ax -- valence angle,
Tx -- torsional angle).
It is important to realize that the torsional angle is undefined if either atoms i, j and k, or j, k and l are collinear (i.e., a straight line is passing through three consecutive atoms) because an infinite number of planes can pass through three collinear points. For this reason, it does not make sense to talk about a torsional angle in acetylene.
An important property of torsional angles is that they do not depend
upon the end from which they are measured, i.e.,
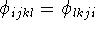 . This stems from the same basic principle
of geometry as the fact that a DNA strand
is a right-handed helix irrespective
from which terminus you look at it. You are encouraged to explore torsional
angle
properties with a bent paper clip or a folded piece of cardboard since this
concept is essential for efficient work with any molecular modeling
software system.
. This stems from the same basic principle
of geometry as the fact that a DNA strand
is a right-handed helix irrespective
from which terminus you look at it. You are encouraged to explore torsional
angle
properties with a bent paper clip or a folded piece of cardboard since this
concept is essential for efficient work with any molecular modeling
software system.
To fully specify molecular geometry to the computer in cartesian coordinates for a molecule containing N atoms, 3N values must be entered (i.e., X, Y and Z for each atom). The 3N coordinates specify not only intramolecular distances and angles but also the orientation of the molecule in space. Internal coordinates, on the other hand, specify only intramolecular distances and angles and the spatial orientation of the molecule is usually assumed. The popular way of specyfying molecular geometry using internal coordinates is a Z-matrix convention (see Fig. 6.12). Each line of the Z-matrix, with the exception of the first 3 lines, has the following format:
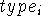 , j,
, j, 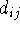 , k,
, k, 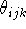 l,
l, 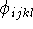
where i is the number of the atom whose position is being defined.
Since atoms are numbered consecutively, this number is equal to the current
Z-matrix row number and this entry is
often used for some mnemonic symbol for an atom or simply omitted as
being redundant. The next entry, 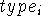 , is the atom type
being defined (e.g., the atomic number), and
j, k, and l refer to atoms whose positions were already defined in
previous
lines of the Z-matrix. The
, is the atom type
being defined (e.g., the atomic number), and
j, k, and l refer to atoms whose positions were already defined in
previous
lines of the Z-matrix. The 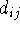 ,
, 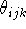 and
and 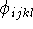 are:
bond length, valence angle and torsional angle, respectively, formed
by atom i with the corresponding atoms. In fact, in many cases,
are:
bond length, valence angle and torsional angle, respectively, formed
by atom i with the corresponding atoms. In fact, in many cases, 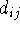 ,
,
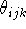 and
and 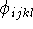 need not be measured along chemical
bonds but simply represent a purely geometrical relationship of atom i
with previously defined atoms. The first three lines of the Z-matrix are
shorter, because there is yet not enough defined atoms to specify
distances and angles. The first line contains only the type of the first
atom being defined,
need not be measured along chemical
bonds but simply represent a purely geometrical relationship of atom i
with previously defined atoms. The first three lines of the Z-matrix are
shorter, because there is yet not enough defined atoms to specify
distances and angles. The first line contains only the type of the first
atom being defined, 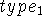 .
By convention, this atom is placed at the origin of the coordinate system.
The second line, in addition to the atom type of the second atom,
contains the distance from the first atom,
.
By convention, this atom is placed at the origin of the coordinate system.
The second line, in addition to the atom type of the second atom,
contains the distance from the first atom, 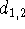 .
It is assumed by convention that bond 1--2 lies along the z-axis
and points upwards towards the positive values of z. The third line
contains
.
It is assumed by convention that bond 1--2 lies along the z-axis
and points upwards towards the positive values of z. The third line
contains 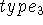 as well as a distance d and an angle
as well as a distance d and an angle 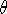 for the
third atom
with respect to atoms 1 and 2. It is generally accepted that
the third atom lies in the positive quadrant
of the plane formed by the x and z axes. Some software packages adopt
slightly different conventions for the Z-matrix (e.g., order of entries
on the input line), incorporate a larger
menu of internal coordinates (e.g., improper torsions, ring closures,
etc.), and may contain some other information (e.g., atomic charges)
together with the entries described above.
for the
third atom
with respect to atoms 1 and 2. It is generally accepted that
the third atom lies in the positive quadrant
of the plane formed by the x and z axes. Some software packages adopt
slightly different conventions for the Z-matrix (e.g., order of entries
on the input line), incorporate a larger
menu of internal coordinates (e.g., improper torsions, ring closures,
etc.), and may contain some other information (e.g., atomic charges)
together with the entries described above.
A Z-matrix requires only 3N-6 parameters (internal coordinates) for a full specification of molecular geometry (0 in first line, 1 in the second line, 2 in the third line, and 3(N-3) in the next N-3 lines). This is because the orientation of the molecule described by the Z-matrix is predefined, otherwise 6 additional parameters are needed to describe the orientation of a non-linear object in space (3 translational and 3 rotational degrees of freedom). In specifying internal geometry with a Z-matrix, dummy atoms are frequently used. Dummy atoms allow the specification of orientation other than the one dictated by the current convention for Z-matrix. They also must be used sometimes to account for collinear atoms in the molecule to avoid undefined torsional angles.
Cartesian coordinates are used as an input for many molecular modeling
software systems. The particular format depends on the system being used.
The most popular format used to describe the structure of a macromolecule
is a PDB file. A full description
of the format of this file is available from Protein Data Bank at
Brookhaven National Laboratory. All molecular modeling systems
designed to work with biopolymers are capable of reading and
producing files in this format. It is not well suited to
represent small molecules, but on the other hand, no standard is
generally accepted to describe the structure of small molecules. Therefore
the PDB format needs be used sometimes as a vehicle to pass molecular
structure information between software of different authors.
A fragment of a PDB file is shown in Fig. 6.13. The file consists of
records (lines), each 80 characters long. Each record (line) consists of
a few fields. The last field at columns 71-80, contains
the PDB file name and an ordinal number for the current record.
The structure of
records is fixed, i.e., each field starts at a prescribed column
and has a strict format (e.g., number of decimal places). Some records
have to follow in a strict order. Each record starts with a keyword which
identifies the type of information in this record. Most keywords are
self-explanatory and only few will be explained here.
file. A full description
of the format of this file is available from Protein Data Bank at
Brookhaven National Laboratory. All molecular modeling systems
designed to work with biopolymers are capable of reading and
producing files in this format. It is not well suited to
represent small molecules, but on the other hand, no standard is
generally accepted to describe the structure of small molecules. Therefore
the PDB format needs be used sometimes as a vehicle to pass molecular
structure information between software of different authors.
A fragment of a PDB file is shown in Fig. 6.13. The file consists of
records (lines), each 80 characters long. Each record (line) consists of
a few fields. The last field at columns 71-80, contains
the PDB file name and an ordinal number for the current record.
The structure of
records is fixed, i.e., each field starts at a prescribed column
and has a strict format (e.g., number of decimal places). Some records
have to follow in a strict order. Each record starts with a keyword which
identifies the type of information in this record. Most keywords are
self-explanatory and only few will be explained here.
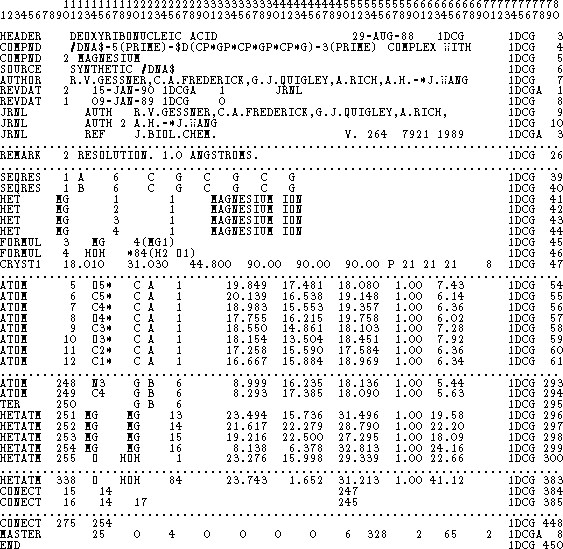
Figure 6.13: Fragment of a PDB file for an oligonucleotide.
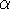 ,
, 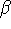 and
and 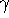 in degrees; and
crystallographic space group.
in degrees; and
crystallographic space group.In most cases the hydrogen atoms are not listed in the PDB file, since they are usually below the resolution of X-ray crystallography. Molecular modeling systems find the approximate positions of hydrogen atoms based on positions of heavy atoms, and therefore, PDB files processed by the modeling software may have these atoms appended.