
Next: Concluding Remarks Up: Results and Discussion Previous: Geometries
Proton Affinities
Total energies calculated by different quantum approaches are listed
in Table V.
Direct comparison of absolute total energies calculated by different methods
used in this work is only possible among the results obtained by the same
program. For ab initio, as expected,
the inclusion of six d-type polarization functions
(in the DH6D basis set), compared with five pure d-type functions (in the
DH5D basis set)
lowers the calculated energy. Using six cartesian d-type gaussians
is equivalent to using the set of five pure functions of d-type augmented with
a 3s-type (i.e., 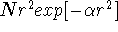 ) function.
This energy change is negligible for our RHF calculations
(on average 0.00060 hartree, i.e.,
) function.
This energy change is negligible for our RHF calculations
(on average 0.00060 hartree, i.e.,  0.38 kcal/mol), however,
this change is roughly 10 times larger
(on average 0.0059 hartree, i.e.,
0.38 kcal/mol), however,
this change is roughly 10 times larger
(on average 0.0059 hartree, i.e.,  3.7 kcal/mol)
for MP2 calculations. This reflects the
fact that polarization functions contribute substantially
to low-lying virtual orbitals, and the contamination with
the 3s orbital brought by combination of six cartesian d-type functions
is expressed much more strongly in correlated methods than at the
RHF level. On the other hand, the difference between corresponding MP2(5d)
and MP2(6d) energies is essentially identical for the parent
and protonated molecule
thus, this basis set modification
does not significantly affect the electronic energy contribution,
3.7 kcal/mol)
for MP2 calculations. This reflects the
fact that polarization functions contribute substantially
to low-lying virtual orbitals, and the contamination with
the 3s orbital brought by combination of six cartesian d-type functions
is expressed much more strongly in correlated methods than at the
RHF level. On the other hand, the difference between corresponding MP2(5d)
and MP2(6d) energies is essentially identical for the parent
and protonated molecule
thus, this basis set modification
does not significantly affect the electronic energy contribution,
 , to the calculated proton affinity.
This should be expected since
the parent and the protonated molecule have the same number of ``heavy''
atoms whose basis sets contain d-type functions and they differ only
in the number of hydrogen atoms.
, to the calculated proton affinity.
This should be expected since
the parent and the protonated molecule have the same number of ``heavy''
atoms whose basis sets contain d-type functions and they differ only
in the number of hydrogen atoms.
The effect of adding Becke-Perdew corrections to the LSD energy can be
examined for DGauss and deMon calculations. It is known that LSD approximation
tends to grossly overestimate correlation energy (frequently as much as 100%)
while it underestimates electron exchange energy by as much as 10%  .
Both, the exchange and the correlation energy, are negative but typically
the magnitude of electron exchange energy is of several orders of magnitude
larger than the correlation energy for the same system. Therefore, the
magnitude of the 10% correction to the exchange energy is typically
larger than the magnitude of the correlation energy. For this reason,
NLSD corrected energies are lower than the corresponding LSD energies.
.
Both, the exchange and the correlation energy, are negative but typically
the magnitude of electron exchange energy is of several orders of magnitude
larger than the correlation energy for the same system. Therefore, the
magnitude of the 10% correction to the exchange energy is typically
larger than the magnitude of the correlation energy. For this reason,
NLSD corrected energies are lower than the corresponding LSD energies.
DMol uses five d-type functions) while DGauss and deMon use six cartesian gaussians as d-type functions. Judging from ab initio results, this difference should not have any substantial impact on the calculated proton affinities.
The changes in the ground state electronic energies on protonation,
 , are ordered as:
DMol < DGauss(LSD)
, are ordered as:
DMol < DGauss(LSD)  deMon(LSD) <
DGauss(NLSD)
deMon(LSD) <
DGauss(NLSD)  deMon(NLSD) < MP2(6d)
deMon(NLSD) < MP2(6d)  MP2(5d)
< RHF(6d)
MP2(5d)
< RHF(6d)  RHF(5d).
This finding suggests that the LSD approximation
generally underestimates electronic energy changes on protonation,
and gradient (NLSD) corrections bring the results significantly closer
to the MP2 values.
RHF(5d).
This finding suggests that the LSD approximation
generally underestimates electronic energy changes on protonation,
and gradient (NLSD) corrections bring the results significantly closer
to the MP2 values.
The DH5D and DH6D basis sets are far from optimal for calculations
of proton affinities since they do not include diffuse s and p-type
functions  . It is dramatically pronounced in the calculated energies
for anions. However, they were chosen here for comparison with DFT
calculations.
Inclusion of diffuse functions is absolutely required
. It is dramatically pronounced in the calculated energies
for anions. However, they were chosen here for comparison with DFT
calculations.
Inclusion of diffuse functions is absolutely required  for meaningful calculations of electronic energy for anions by ab initio
methods..
To illustrate the effect of diffuse functions, we performed
RHF and MP2 calculations for formate anion,
and the corresponding neutral acid with DH6D basis set
augmented with diffuse s-type and p-type functions
on oxygen atoms. As expected, this led to a substantial lowering of
electronic energy for the formate anion, while the effect was much
smaller for the neutral acid, i.e., the
for meaningful calculations of electronic energy for anions by ab initio
methods..
To illustrate the effect of diffuse functions, we performed
RHF and MP2 calculations for formate anion,
and the corresponding neutral acid with DH6D basis set
augmented with diffuse s-type and p-type functions
on oxygen atoms. As expected, this led to a substantial lowering of
electronic energy for the formate anion, while the effect was much
smaller for the neutral acid, i.e., the  was
significantly smaller for the basis sets including diffuse functions.
Surprisingly, the DFT methods seem less sensitive to the lack of diffuse
functions. This apparent insensitivity of the DFT calculations to the
inclusion of diffuse functions may be explained by the fact that
the underlying quantity in the DFT calculation is the charge density.
Diffuse functions do not contribute substantially to the occupied
molecular orbitals, and the charge density is the sum of one-particle
densities derived from the corresponding occupied orbitals.
This reasoning is indirectly supported by our ab initio
results. The HF energy for the formate, is substantially less affected
by adding diffuse functions (0.0110 hartree) than
the MP2 energy (0.0222 hartree). The energies of formic acid
calculated with and without diffuse functions differ by 0.0032 and 0.0090,
for HF and MP2; respectively.
was
significantly smaller for the basis sets including diffuse functions.
Surprisingly, the DFT methods seem less sensitive to the lack of diffuse
functions. This apparent insensitivity of the DFT calculations to the
inclusion of diffuse functions may be explained by the fact that
the underlying quantity in the DFT calculation is the charge density.
Diffuse functions do not contribute substantially to the occupied
molecular orbitals, and the charge density is the sum of one-particle
densities derived from the corresponding occupied orbitals.
This reasoning is indirectly supported by our ab initio
results. The HF energy for the formate, is substantially less affected
by adding diffuse functions (0.0110 hartree) than
the MP2 energy (0.0222 hartree). The energies of formic acid
calculated with and without diffuse functions differ by 0.0032 and 0.0090,
for HF and MP2; respectively.
Table VI collects zero point energies (ZPE) derived from calculated
vibrational frequencies by eq 2, and the temperature-dependent portion
of vibrational enthalpies,  ,
computed from eq 3 for the molecules studied.
All values of
,
computed from eq 3 for the molecules studied.
All values of  are small for molecules of this
size, in our case on the order of 1 kcal/mol or less. Consequently, the
differences between
are small for molecules of this
size, in our case on the order of 1 kcal/mol or less. Consequently, the
differences between  values for the
parent and protonated molecules are
negligibly small compared to the experimental error in proton affinity
measurements.
For larger molecules
values for the
parent and protonated molecules are
negligibly small compared to the experimental error in proton affinity
measurements.
For larger molecules 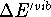 can also be safely
omitted in proton affinity calculations since the largest contributions
to
can also be safely
omitted in proton affinity calculations since the largest contributions
to  come from the lowest frequency vibrations
(e.g., torsions around single bonds) and these are for the most part not
substantially affected by protonation.
come from the lowest frequency vibrations
(e.g., torsions around single bonds) and these are for the most part not
substantially affected by protonation.
The value of ZPE is proportional to the sum of vibrational frequencies,
and therefore it is primarily affected by larger frequences
(e.g., bond stretching and bending vibrations).
The differences in ZPE for protonated and parent molecule
is therefore not small and in our case approaches 10 kcal/mol. Protonation
results in the formation of a new covalent X--H bond and also affects
geometry and strength of vicinal bonds. For that reason,  must be accounted for in proton affinity calculations.
Also, systematic over- or under-estimation of frequencies will
bias the value of ZPE in the same direction.
Moreover, it should be noted that ZPE in our case is calculated
within the harmonic approximation. Experimental frequencies available
in the literature for our series of molecules are not
corrected for anharmonicity, and therefore,
direct comparisons with experimental values of ZPE were
not attempted.
must be accounted for in proton affinity calculations.
Also, systematic over- or under-estimation of frequencies will
bias the value of ZPE in the same direction.
Moreover, it should be noted that ZPE in our case is calculated
within the harmonic approximation. Experimental frequencies available
in the literature for our series of molecules are not
corrected for anharmonicity, and therefore,
direct comparisons with experimental values of ZPE were
not attempted.
The magnitudes of calculated ZPE's in our series of molecules
are ordered as:
DMol  DGauss(LSD)
DGauss(LSD)  deMon(LSD)
deMon(LSD)  deMon(NLSD)
< MP2(6d)
deMon(NLSD)
< MP2(6d)  MP2(5d) < RHF(6d)
MP2(5d) < RHF(6d)  RHF(5d). RHF
frequences are usually larger than experimental
(even if measured frequencies are converted to harmonic ones)
and therefore the RHF calculated ZPE's are too large
RHF(5d). RHF
frequences are usually larger than experimental
(even if measured frequencies are converted to harmonic ones)
and therefore the RHF calculated ZPE's are too large  .
The MP2 calculated frequencies are in much better agreement with
experiment, though in general they are also slightly higher
than measured harmonic frequencies
.
The MP2 calculated frequencies are in much better agreement with
experiment, though in general they are also slightly higher
than measured harmonic frequencies  . This
effect is clearly visible in stretches along polar X--H bonds.
Since LSD calculated
zero point energies are slighlty smaller than MP2 calculated ones,
they exhibit the plausible trend.
RHF and MP2 calculations with the DH6D
. This
effect is clearly visible in stretches along polar X--H bonds.
Since LSD calculated
zero point energies are slighlty smaller than MP2 calculated ones,
they exhibit the plausible trend.
RHF and MP2 calculations with the DH6D 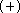 basis set for formic acid,
and the corresponding anion, produced ZPE's very similar to
the DH6D basis set. The major contribution to error in proton affinities
of anions calculated with basis sets lacking diffuse functions is therefore
from the electronic energies.
basis set for formic acid,
and the corresponding anion, produced ZPE's very similar to
the DH6D basis set. The major contribution to error in proton affinities
of anions calculated with basis sets lacking diffuse functions is therefore
from the electronic energies.
Proton affinities were calculated from eq 4. The values of calculated
gas phase proton affinities together with the experimental values
are collected in Table VII. The errors in experimental values are roughly
2 kcal/mol for affinities within 167-204 kcal/mol range and the error
gets much larger outside this range due to the lack of adequate reference
proton affinities 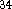 .
.
The RHF(6d) and RHF(5d) calculated proton affinities are practically
identical. In our series of molecules they are all too large compared
to experimental values. Overestimation of proton affinities at the
RHF level is well illustrated by other authors for similar
molecules 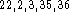 .
This trend in RHF calculations is mainly due to
the overestimated
.
This trend in RHF calculations is mainly due to
the overestimated  , however,
, however,  is
usually also exaggerated since
the calculated frequency of the newly formed X--H bond
is too large. The MP2 results are practically
identical for MP2(6d) and MP2(5d) cases, and are in substantially
better agreement with experimental values. As was mentioned above, adding
diffuse functions on oxygen dramatically improves
the calculated proton affinity for the formate anion.
is
usually also exaggerated since
the calculated frequency of the newly formed X--H bond
is too large. The MP2 results are practically
identical for MP2(6d) and MP2(5d) cases, and are in substantially
better agreement with experimental values. As was mentioned above, adding
diffuse functions on oxygen dramatically improves
the calculated proton affinity for the formate anion.
The proton affinities calculated within the
LSD approximation are substantially smaller than
the experimental values. For our series of molecules, LSD underestimates
 .
Proton affinities calculated with DGauss(NLSD) and deMon(NLSD)
are in excellent agreement with the experimental values.
They are even slightly better
(
.
Proton affinities calculated with DGauss(NLSD) and deMon(NLSD)
are in excellent agreement with the experimental values.
They are even slightly better
(  kcal/mol,
kcal/mol, 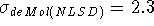 kcal/mol)
then those from MP2 calculations
(
kcal/mol)
then those from MP2 calculations
(  kcal/mol when
the result obtained with diffuse basis functions was used for formate)
and much better
than the ones from RHF calculations (
kcal/mol when
the result obtained with diffuse basis functions was used for formate)
and much better
than the ones from RHF calculations (  kcal/mol).
kcal/mol).
It seems that for this particular series of molecules it does not matter if gradient corrections were applied perturbationally to the LSD energy (at LSD optimized geometry) or if they were introduced in a self-consistent way during geometry optimization. This may, however, be fortuitous due to the fact that C--X bonds are slightly shorter and X--H and C--H slightly longer than for the corresponding NLSD calculations. It may provide for some cancellation of errors which results in similar overall values of affinities.
Next: Concluding Remarks Up: Results and Discussion Previous: Geometries Computational Chemistry
Thu Oct 30 00:15:06 EST 1997
