http://server.ccl.net/cca/documents/proton-affinity/affinities/node2.shtml

CCL node2

About CCL Rules, Instructions, Contributing Material, Supporting, About Us, Resources Software Archive, List Archive, Data Archives, Document Archives, Search CCL Text Search, RegExp Search, Announcements Conferences, Jobs, Resumes, Links Topics, Data, Software Sites, Hardware Sites, Institutions, Listsoftsites, Search Engines, E-mail us Send E-mail to CCL Administrators,

Computational Methods Proton affinity 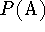is defined as the negative of the molar enthalpy change at 298.15 K ( 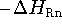) for the reaction A + H AH , or in the case of anions, A + H AH. To calculate these values from theory for gas phase reactions we may, in most cases, obtain adequate results assuming ideal gas behaviour: . 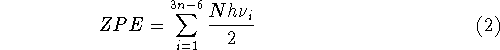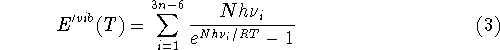Assuming that there is only one conformer present, the energy E(T) of a mole of gas consisting of nonlinear polyatomic molecules can be approximated as : where n denotes the number of atoms in the molecule, ZPE is the zero point energy, represents the temperature dependent portion of vibrational energy, 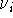are the calculated vibrational frequencies and 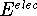is the electronic energy . The change in the energy occuring during protonation of 1 mole of gas at 298.15 K, , will therefore consist of the following components: - the change in rotational energy upon conversion of the reactants to the product. Since a proton does not possess rotational kinetic energy, this term is nonzero only if the protonated molecule has a different fundamental shape than the parent one (e.g., when A is linear and AH is nonlinear). In our case, all parent and protonated molecules are nonlinear, hence, . - the change in energy associated with translational degrees of freedom. Since the proton on the left hand side of the equation brings 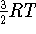, the net ; i.e., for 298.15 K 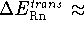0.88873249 kcal/mol. 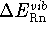- the change in energy associated with internal vibrations of reactants and products. Only the change in the zero point energy, is significant. The 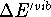is usually much less then 1 kcal/mol at room temperatures (i.e., much smaller than the experimental error) and is included here only for completeness. - the change in the electronic energy upon reaction. In our case it is the difference between ground state energies (electronic + nuclear) taken from quantum calculations with full geometry optimization for the protonated and parent molecules. The ground state energy of a proton is zero in this formulation. Combining the above, the following expression for proton affinity was used in actual computations: The values of 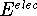and the vibrational frequences 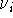were obtained from quantum calculations. Programs Gaussian90 and ACES2 were used for traditional ab initio calculations. The original double-zeta basis set of Dunning/Huzinaga (9s,6p/4s) (6111,411/31) was augmented with polarization functions: d-type on C, N, O with exponents equal to: 0.8, 0.8, and 0.9 respectively, and p-type with an exponent equal to 1.0 for H. Two sets of ab initio calculations were performed. DH6D set used cartesian gaussians (i.e., six d-type functions) and the DH5D set used five d-type functions with the angular part represented by spherical harmonics. These DZP basis sets had similiar characteristics to the basis sets we used in our DFT calculations. The RHF and MP2 calculations were also performed for formic acid and its anion with a DH6D basis set augmented with diffuse s-type and p-type functions (with exponent 0.0845 ) on oxygen atoms. It is well known that adding diffuse functions on nonhydrogen atoms dramatically improves results for proton affinities though it is less important for molecular geometry. This basis set is referred to later as DH6D 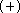. The ab initio results were compared with those obtained from DFT calculations performed with the programs: DGauss 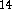, DMol and an academic version of deMon 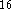. The DGauss and deMon programs use the LSD potential developed by Vosco et al. 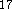while DMol incorporates the Barth and Hedin LSD potential 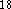. Basis sets of double-zeta quality with polarization functions were used in all DFT programs. In DMol, the DNP (Double Numerical with Polarization) basis set included with the program was selected. The basis sets in this program are given numerically as cubic spline functions. The 300 radial points spaning a range from nucleus to an outer distance of 10 bohrs is a default. The angular portion of each basis function corresponds to the appropriate spherical harmonic. The DGauss and deMon basis functions are analogous to those widely used in traditional ab initio calculations, i.e., they are represented analytically by a combination of primitive gaussian functions; however, they have been reoptimized for the DFT calculations 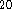. For DGauss and deMon DZVP atomic basis set and A2 auxiliary fitting set was used for 1st row atoms and DZVPP/A1 set for hydrogens. The contraction pattern for the atomic basis set was (9s,5p,1d/5s,1p) (621,41,1/41,1). In other words, for 1st row atoms there were three s-type basis functions combining six, two, and one gaussian primitives, respectively; two sets of p-type basis functions containing four and one primitives, and a single primitive for each of the six d-type polarization functions 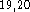. For hydrogens two s-type functions combining four and one gaussian primitives, and p-type polarization functions consisting of one gaussian were used as a basis set. Beside atomic basis set, in DGauss and deMon, auxiliary sets of functions are used to fit charge density and exchange-correlation potential 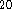. For each atom there is one set for fitting density and another set for fitting exchange-correlation potential. The sets consist of uncontracted s-type gaussians and a few groups of s, p, and d-type cartesian gaussians sharing the same exponent. The composition of these sets is denoted as (A,B;C,D), where A,B pair specifies that A s-type gaussians, and B groups of spd gaussians were used for fitting density, and C s-type gaussians and D groups of spd gaussians were used to fit exchange-correlation potential. The A2 auxiliary set was denoted (4,4;4,4), while the smaller A1 set used for hydrogens was (3,1;3,1). Starting geometries for molecules were obtained from model building with Sybyl using previous computational results 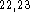and experimental data 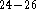. Geometries of protonated molecules were obtained by placing a proton at position of the lone electron pair of the accepting atom. The X-H bond lengths from the corresponding unprotonated molecules were used for these new bonds as starting values. These geometries were then fully optimized within given method. It was absolutely necessary since these final geometries were used for normal modes and vibrational frequency calculations. Atom numbering used throughout this paper is shown in Figure 1 which was produced with the MindTool software . Ab initio geometry optimizations were performed in DIRECT SCF mode with Gaussian90, and the resulting geometries were used with ACES2 for vibrational frequency and normal mode calculations. ACES2 computes normal modes and frequencies from the analytical Hessian for RHF and MP2 calculations. We also performed geometry optimizations at the MP2 level (full core) with Gaussian90 in an analogous manner, followed by frequency calculations with ACES2. In the MP2 case we used the RHF-optimized geometries as starting data. The DFT calculations with both DGauss and DMol were carried out with full geometry optimization at the Local Spin Density (LSD) level. Geometry optimizations with nonlocal gradient corrections were performed with deMon. Geometry optimization was followed by frequency calculations. For all DFT codes the Hessian needed for frequency and normal modes evaluation was calculated from analytical energy gradients by finite differences with a step of 0.01 bohr. Integration grid in DGauss and deMon was of similar quality (MEDIUM and FINE respectively). In DMol the FINE integration grid density was used and the the maximum angular momentum number (LMAX) of the multipolar functions used to analitically fit electron density and exchange-correlation potential was 2 for hydrogens and 3 for other atoms. Nonlocal density gradient corrections to the LSD energies were not available in this version of DMol. The version of DGauss used by us provided for single-point nonlocal gradient corrections to LSD energies, while the deMon program offered gradients of nonlocal gradient corrections, i.e., provided for geometry optimization at this level. Based on our previous experience , we chose the Becke 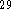functional for the exchange and Perdew functional for the correlation potential, which we label Becke-Perdew corrections. The Becke-Perdew corrections were shown to improve results compared to LSD approximation . Since gradients of gradient-corrected energies could not be calculated with this version of DGauss, single-point corrected energies were calculated for the LSD-optimized geometries and vibrational contributions to proton affinities were assumed to be the same as for the LSD. For deMon, the fully-consistent LSD and NLSD results are reported.

[ CCL Home Page ]
[ About CCL ] [ Resources ] [ Search CCL ] [ Announcements ] [ Links ] [ E-mail us ]
[ Raw Version of this page ]

Modified: Thu Oct 30 17:00:00 1997 GMT

Page accessed 2492 times since Thu Jun 10 06:41:10 1999 GMT