Introduction

Protonation reactions, i.e., A + H tex2html_wrap_inline406 tex2html_wrap_inline408 AH , are among the most important in chemistry and biology. Protonation/deprotonation is the first step in many fundamental chemical rearrangements and in most enzymatic reactions. Two quantities are used to characterize the ability of a molecule in the gas phase to accept a proton. The gas phase basicity is the negative of the free energy change associated with the reaction. The more frequently used index, the proton affinity, is the negative of the enthalpy change at standard conditions. Experimental determination of these parameters is not easy (for an excellent review on this topic see Dixon and Lias tex2html_wrap_inline412 ), and with the phenomenal growth in computer power in recent years, much attention has been given to the possibility of calculating these parameters by quantum methods. Ab initio approaches are very successful in providing reliable values of proton affinities and gas phase basicities for small molecules even at lower levels of theory tex2html_wrap_inline414 . However, due to computational expense, application of ab initio methods to the estimation of proton affinities is still impractical for larger molecules. Semiempirical methods such as AM1, MNDO and PM3, are not consistently reliable in calculations of proton affinities as shown by Ozment and Schmiedekamp tex2html_wrap_inline416 .

The recent progress in the Density Functional Theory (DFT) approaches (for review see refs 4-6) make this method another candidate for reliable calculation of proton affinities, however, the performance of the method in this field is still mostly untested. This prompted us to analyze its performance on a few representative molecules spanning a wide range of proton affinity values.

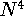DFT methods are computationally less demanding than correlated ab initio approaches and formally scale with the size of the molecule as tex2html_wrap_inline418 or tex2html_wrap_inline420 , depending on implementation. For the the simplest Hartree-Fock ab initio approach the scaling is 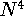. Moreover, the advantage of DFT methods is that they should in principle include electron correlation energy via the correlation/exchange potential, while the Hartree-Fock approach by definition does not include this component of energy. 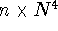The simplest of the routinely-used ab initio correlated approaches, based on the second order many body perturbation theory, MBPT(2) (frequently called second order Møller-Plesset theory - MP2), recovers only a portion of the correlation energy and scales as tex2html_wrap_inline424 (n is the number of occupied molecular orbitals). The major weakness of DFT approaches is that the exact mathematical form of the exchange-correlation potential is not known. For that reason approximations are used. The most popular is the Local Spin Density (LSD) approximation, which simply assumes that the exchange-correlation potential dependence upon charge density is represented by the functional form found for the homogenous electron gas. This approximation works well in many cases; however, it suffers from severly underestimating electron exchange tex2html_wrap_inline428 and overestimating the correlation energy tex2html_wrap_inline430 . Appropriate corrections to the local density approximation are therefore sought, and several of such schemes already exist tex2html_wrap_inline432 .

Next: Computational Methods Up: No Title Previous: No Title

Computational Chemistry
Thu Oct 30 00:15:06 EST 1997

[ CCL Home Page ]
[ About CCL ] [ Resources ] [ Search CCL ] [ Announcements ] [ Links ] [ E-mail us ]
[ Raw Version of this page ]

Modified: Fri Aug 4 17:27:25 2000 GMT

Page accessed 2455 times since Thu Jun 10 06:41:03 1999 GMT